Bevezetés
Minden kísérletes tudomány esetén felmerül a vizsgált jelenség kvalitatív vizsgálatán túl kvantitatív vizsgálat, azaz a mérések szükségessége. A kísérlet megtervezésén túl fontos feladat a nyert adatok megfelelő feldolgozása és kiértékelése. Teki
ntsünk néhány tipikus problémát.1. Kísérleti állatok testsúlyának a változását vizsgálták bizonyos gyógyszerek beadása után. Az A gyógyszer alkalmazása után 25 állatnál átlagosan 5%-os emelkedést figyeltek meg. A B gyógyszer 10 állatra alkalmazva, 3%-os növekedést eredményezett. Hatásosabb-e az A szer? Az 5% és a 3% nem ad gyakorlati választ a kérdésre, mivel az alacsonyabb értéket okozhatta egy állat is, amely -valamilyen oknál fogva- fogyott. Ezért vizsgálnunk kell az egyedi súlyok eloszlását és szóródásukat az átlag körül. El kell dönteni továbbá, hogy a kísérleti állatok száma elegendő-e ahhoz, hogy a két szer hatását adott biztonsággal különbözőnek tekintsük.
2. Egy bizonyos kísérleti eredményről el kell döntenünk, hogy az ellentmond-e megelőző kísérletekből származó eredménynek vagy valamilyen elméleti értéknek. A kísérletet ilyenkor hipotézis tesztelésére használjuk.
3. A mért változók ismert egy törvényszerű, egyenlettel megadott kapcsolat, de az egyenlet paraméterét a kísérletből kell meghatározn
i. Pl. a rádióaktív bomlás esetén az N(t)=C• e-l t egyenlet adja meg a t idő alatt elbomlott atomok számát. A l konstanst és mérési hibáját megfigyelések N1(t1), N2(t2), .... sorozatából kell meghatározni. Ez az ún. paraméterbecslés talán az egyik legérdekesebb probléma sok kutató számára.Ezekből a példákból látható az adatfeldolgozás néhány jellemzője. Látható, hogy egy kísérlet kimenetelét nem határozzák meg egyértelműen a kísérlet feltételei, hanem a véletlentől is függ: a kísérlet eredménye ún. véletlen változó vagy valószínűségi változó. Ez a véletlen tendencia a kísérlet természetéből fakadhat ( a tesztelendő állatok különböznek, a rádioaktivitás is sztachasztikus jelenség), vagy a mérési hiba következménye. A következő fejezetben ezért áttekintést adunk a valószínűségszámítás alapjair
ól.Ezután valószínűségi változókról lesz szó, ezek eloszlásáról és az eloszlások paramétereiről átlagról, varianciár
ól. Néhány fontosabb eloszlást bemutatunk, különös tekintettel a normális vagy Gauss féle eloszlásra.
.
.
.
I. A valószínűségelmélet alapjai
Kísérlet, esemény
Mivel kísérletekből származó adatokkal foglalkozunk, először megállapítjuk, mit értünk kísérleten és mit az eredményén. Véletlen kísérleten olyan kísérletet értünk, amelynek kimenetelét az általunk figyelembe vett feltételek nem határozzák meg egyértelműen.
Véletlen kísérlet pld. egy pénz vagy egy kocka feldobása, egy oldat koncentrációjának megmérése, egy kísérleti állat testsúlyának a megmérése, stb.Minden kísérletnek van tehát több, esetleg végtelen sok lehetséges kimenetele. Ha a kísérlet egy pénz feldobása, akkor két lehetséges kimenetel van, a "fej" vagy az "írás", a kockadobás esetén 6 lehetséges kimenetel van, koncentrációmérés esetén annyi lehetséges kimenetel van, amennyi valós szám van 0 és 100 között, a testsúlymérésnél annyi lehetséges kimenetel van, amennyi valós szám elképzelhető 0 és egy ésszerű felső határ között. Ha egy kísérletnek véges sok és nem túl nagyszámú kimenetele van, akkor elég sok kísérlet esetén ezek konkrétan megvalósulnak. Ha azonban a kísérletnek végtelen sok kimenetele van, közülük csak véges sok realizálódhat, egyesek tehát soha nem jönnek létre. Ettől függe
tlenül ezeket is gondolatban számontartjuk, mint lehetséges kimeneteleket.Egy kísérlet eredményét eseménynek nevezzük . Az eseményeket nagybetűkkel jelöljük(A,B,E, stb.). Az események lehetnek elemiek vagy összetettek.
Egy kísérlet lehetséges kimeneteleit elemi eseményeknek nevezzük. Egy kísérlethez tartozó elemi események összességét eseménytérnek nevezzük és W -val jelöljük.
Egy eseményt összetett eseménynek nevezzük, ha felbontható további részeseményekre, végső soron elemi eseményekre. Az összetett események az eseménytér részhalmazai. Egy eseményt biztos eseménynek nevezünk, ha a kísérlet feltételeitől függetlenül mindig bekövetkezik (W ) . Egy eseményt lehetetlen eseménynek nevezünk, ha sohasem következik be, jele: Æ
Példák:
1. Tekintsük a pénzdobálás kísérletét. Az elemi események: Æ , F,I, W . A biztos esemény ( ) : a kimenetel fej vagy írás.
2. A kísérlet két pénzérme feldobása. Az elemi események a következők:
az első fej, a második is fej: (F,F)
az első fej, a második írás: (F,I)
az első írás, a második fej: (I,F)
az első írás, a második is írás: (I,I)
3. A kockadobásnál az elemi események a felső lapon látható számok: 1,2,3,4,5,6.
Példák eseményekre:
E1={1,3,5} (az eredmény páratlan szám).
E2={2,4,6} (az eredmény páros szám).
E3={5,6} (az eredmény nagyobb, mint 4).
={1,2,3,4,5,6}(biztos esemény).
Műveletek eseményekkel
Egy A esemény komplementere az az esemény, amely akkor következik be, amikor A nem következik be. Az A esemény komplementerét ![]() -sal jelöljük.
-sal jelöljük.
Például:
![]() =
=![]() ={2,4,6}
={2,4,6}
![]() ={1,2,3,4}
={1,2,3,4}
![]() =
=
Két esemény (A és B) összege az az A+B esemény, amely akkor következik be, amikor A vagy B bekövetkezik. A+B pontosan azokat az elemi eseményeket tartalmazza, amelyeket legalább az egyik esemény tartalmaz.
Példák:
E1+E2={1,3,5}+{2,4,6}={1,2,3,4,5,6}
E1+E3={1,3,5}+{5,6}={1,3,5,6}
Két esemény, (A és B) szorzata az az A• B esemény, amely akkor következik be, ha A is és B is bekövetkezik. Az A• B esemény azoknak az elemi eseményeknek a halmaza, amelyek mindkét eseményben egyidejűleg benne vannak.
Példák:
E1• E2={1,3,5}• {2,4,6}=
E1• E3={1,3,5}• {5,6}={5}
E2• E3={2,4,6}• {5,6}={6}
Ha A• B = , akkor azt mondjuk, hogy A és B kizáró események vagy kölcsönösen kizárják egymást. Például E1 és E2 egymást kizáró események, mivel egyidejűleg soha nem következhetnek be.
A valószínűség koncepciója
Bizonyos kísérletek közel azonos körülmények között akárhányszor megismételhetők. Ismételjünk meg egy kísérletet n-szer. Tegyük fel, hogy egy kísérlet n számú kísérletből az A esemény k -szor következik be (![]() ). k-t az A esemény gyakoriságának nevezzük. A
). k-t az A esemény gyakoriságának nevezzük. A
h = ![]()
hányadost az A esemény relatív gyakoriságának nevezzük. Ha n nagy, tehát a kísérletet sokszor megismételjük, a tapasztalat szerint h egy adott szám körül fog stabilizálódni. Ezt a számot nevezzük az A esemény valószínűségének és P(A)-val jelöljük. Mivel ![]() , P(A) szintén 0 és 1 közé esik.
, P(A) szintén 0 és 1 közé esik.
Például: tekintsük a pénzdobálási kísérletet. Vizsgáljuk pl. a "fej" gyakoriságait és a relatív gyakoriságait, ha 10, 100, 1000, 10000 -szer dobjuk fel a pénzt. A következő táblázat mutat egy lehetséges kapott eredményt.
n= 10 100 1000 10000 100000
k= 7 42 510 5005 49998
h= 0.7 0.42 0.51 0.5005 0.49998
Látható, hogy n növekedésével a h egyre jobban stabilizálódik 0.5 körül. Eszerint annak valószínűsége, hogy a pénzfeldobás eredménye fej, 0.5. Jelölése: P(F)=0.5.
A valószínűség axiómái
A valószínűség fenti definíciója a gyakorlati célokra általában megfelelő, de matematikailag nem elegendő. Ezzel a definícióval az az egyik nehézség, hogy végtelen sok kísérletekre van szükségünk, amelyeket természetesen lehetetlen végrehajtani. A valószínűségelmélet axiómatikus megalapozása Kolmogorovtól (1933) származik. (Az axióma egy olyan alapszabály, amelyet alá lehet támasztani, de nem lehet bizonyítani.)
Egy esemény relatív gyakorisága a 0 és 1 számok közé esik. Ez az alapja a következő axiómának:
1. Axióma. Bármely A eseményhez a lehetséges kimenetek teréből hozzá van rendelve egy valós szám, amelyet az A esemény valószínűségének nevezünk és P(A)-val jelölünk. A valószínűség mindig 0 és 1 közé esik: ![]() .
.
A lehetséges kimenetelek W halmaza , azaz a biztos esemény mindig bekövetkezik, így relatív gyakorisága 1.
2.Axióma. A biztos eseményhez az 1 valószínűséget rendeljük hozzá: P(W )=1.
Tapasztalat szerint ha az A és B esemény kölcsönösen kizárja egymást, akkor az A+B esemény relatív gyakorisága az A és B eseményekhez tartozó relatív gyakoriságok összege.
3.Axióma. Ha A és B kölcsönösen kizárják egymást, azaz A• B =Æ , akkor :
P(A+B)=P(A)+P(B).
Következmények. A felsorolt következmények az axiómák alapján bizonyíthatók.
1.Minden A eseményre igaz, hogy P(A)=![]() .
.
2.A lehetetlen esemény valószínűsége 0, azaz P(Æ
)=0.3.Ha A1,A2,...An egymást páronként kizáró események, azaz P(AiAj)=0, ![]() , akkor
, akkor
![]()
4. Tetszőleges A és B eseménypárra érvényes az alábbi egyenlőség:
P(A+B)=P(A)+P(B)-P(AB)
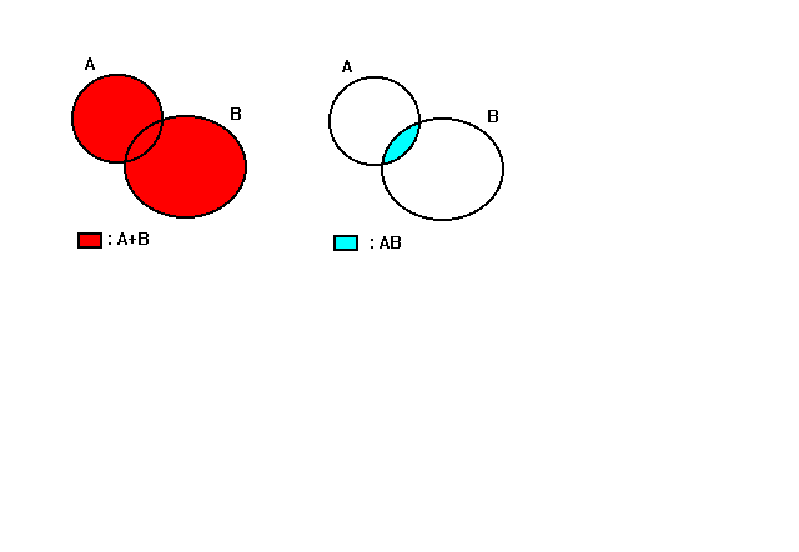
1. ábra
A valószínűség kiszámítása
Tekintsük a pénzdobálási kísérletet. Ha az érme szabályos, kérdezhetjük, hogy mi a fejdobás valószínűsége, ha csak egyszer dobjuk fel az érmét. A "sejtésünk" az, hogy 0.5. Ez a sejtés azon a feltevésen alapul, hogy az eseménytér minden elemi eseménye egyformán valószínű, és a biztos esemény valószínűsége 1.
Általánosan, tegyük fel, hogy egy kísérletnek T számú lehetséges kimenetele van (T számú elemi esemény), ezek egyenlő valószínűséggel következnek be, valamint egy A esemény bekövetkezése szempontjából F számú eset jöhet számításba. Ekkor az A esemény valószínűségét a következő módon számíthatjuk ki:
P(A)=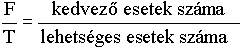 .
.
Példák:
1. Egyszer feldobva egy dobókockát mi a 6-os dobás valószínűsége? Ha X jelöli a dobás eredményét, akkor P(X=5)=1/6, mivel a lehetséges esetek száma 6, és a kedvező eset csak egyféleképpen lehetséges.
2. Mi annak a valószínűsége
, hogy páros számot dobunk? P(páros)=1/2. Itt F=3, T=6, így F/T=3/6=1/2.Feltételes valószínűség
Legyen adott két esemény, A és B (P(B)>0). Végezzük el n-szer egymástól függetlenül azt a kísérletet, amellyel ez a két esemény kapcsolatos. Válasszuk ki azokat az eseteket, amelyekben az A esemény bekövetkezett. Ezek száma kA, az A esemény gyakorisága. Ez utóbbi esetek némelyikében a B esemény is bekövetkezett, ezek száma kAB. E két gyakoriság hányadosa stabilitást mutat, ha a kísérletek számát növeljük. Elvégezve az n-nel való osztást :
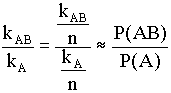
A P(AB)/P(A) számot a B eseménynek az A eseményre vonatkoztatott feltételes valószínűségének nevezzük és a következőképpen jelöljük:
|
P(B A) = |
(1.1) |
Következésképpen
P(AB)=P(A) P(B| A) . |
(1.2) |
Például az 1. ábráról látható, hogy ez egy észszerű definíció. Ha az egyes tartományok területét a megfelelő események valószínűségével arányosnak tételzzük fel, akkor a B esemény valószínűsége az A feltétel mellett valóban arányos az AB és az A területek arányával.
Példa. Húzzunk ki két kártyát, C1-et és C2-t egy 52 kártyát tartalmazó pakliból. Jelölje A azt az eseményt, hogy C1 kőr, B pedig azt, hogy a C2 kőr. Nyilván P(A)=13/52 (összesen 13 ilyen kártya van). Továbbá, ha A bekövetkezett, C2-t már csak 51 kártya közül húzhatjuk ki, melyek között már csak 12 kőr lehet. Tehát P(B|A)=12/51. Annak valószínűsége, hogy mindkét kártya kőr,
P(AB)=P(A) P(B|A)=![]()
Események függetlensége.
Az A és B eseményeket függetlennek nevezzük egymástól, ha
P(B| A) = P(B) |
(1.3) |
vagy, (1.3)-at (1.2)-be helyettesítve
P(AB)=P(A)P(B).
Tehát független események szorzatának valószínűsége a valószínűségeik szorzata.
Példa: Módosítsuk az előző példabeli kísérletet úgy, hogy C
1-et és C2-t két különböző csomagból húzzuk ki. Így A és B események függetlenek lesznek, és így annak valószínűsége, hogy mindkettő kőr, ebben az esetben![]()
Feladatok
1. Egy kockát feldobva 6 lehetséges kimenetel van, Ha X jelöli a dobás eredményét, számítsuk ki a következő valószínűségeket:
a) P(X=1); b) P(X>1); c) P(1<X<4)
2. Egy pénzérmét kétszer egymás után feldobunk. Soroljuk fel az elemi eseményeket! Mi annak a valószínűsége, hogy mindkét dobás írás?
3. Egy pénzt és egy kockát feldobunk. A lehetséges kimenetelek a következők: F1,F2,F3,F4,F5,F6,I1,I2,I3,I4,I5,I6. Számítsuk ki a következő események valószínűségét:
a) fej és páros dobás a kockával
b) fej vagy páros dobás a kockával
c) fej és 5-ös dobás
d) fej vagy 5-ös dobás
e) 4-es vagy 6-os dobás.
4. Szisztolés vérnyomás mérésekor a következő elemi események között teszünk különbséget:
A: a vérnyomás kisebb, mint 120 mm
B: a vérnyomás 120 mm és 150 mm között van
C: a vérnyomás nagyobb, mint 150 mm.
A lehetséges kimenetelek tere {A,B,C}. Adjuk meg az összetett eseményeket!
5. Jelölje x a glukóz súlyát 100 ml vérplazmában. Legyen x1 és x2 két rögzített érték (x1<x2). Legyenek A,B,C,D a következő események:
A: x<x1, B: x>x1, C: x<x2, D: x>x2.
Mely események zárják ki egymást?
6. 15 kísérleti egér testsúlyát mérték meg . A következő grammokban kifejezett súlyokat kapták:
28 31 26 26 29 31 30 27 25 30 28 28 23 32 30
Mi a következő események relatív gyakorisága (x jelöli az aktuális testsúlyt):
E: x<26, F: x=31, G: 26<x<31?
Valószínűségi változók és eloszlásuk
A kísérletek legnagyobb része olyan, hogy az eredményéhez (tehát egy elemi eseményhez) egy szám rendelhető. Ez a szám függ a kísérlettől, a kísérletet azonos körülmények között megismételve más és más elemi esemény következik be, ennek megfelelően adatainkban is véletlen ingadozásokat tapasztalunk. Emléleztetünk arra, hogy az elemi esemény számunkra nem a kísérlet során fizikai értelemben létrejött eseményt jelenti, hanem a kísérlet egy lehetséges végeredményét jellemző absztrakt elemet. Az elemi események akkor is léteznek, ha a kísérletet nem hajtjuk végre. Az egyes számértékeket a kísérlet végrehajtása nélkül is hozzárendelhetjük az egyes el
emi eseményekhez, teljessé téve a szóban forgó kísérlet matematikai modelljét. Így jutunk el a valószínűségi változó fogalmához.Definíció.
Valószínűségi változónak egy, az elemi események W
={w 1,w 2,...} halmazán értelmezett függvényt nevezünk. A valószínűségi változókat nagybetűkkel fogjuk jelölni: X: W ® R, vagy , wTehát egy függvényt valószínűségi változónak nevezünk, ha az egy elemi eseményhez egy valós számot rendel.n
Példák:
1. A kísérlet a pénzdobálás. Két elemi esemény van, a fej és az írás. W ={F,I}.Hozzárendelhetjük például a fej eseményhez a 0 számot és az íráshoz az 1-est. Ekkor az X valószínűségi változónak két értéke van: X(F)=0 és X(I)=1.
2. Ugyanazon kísérlet esetén definiálhatunk más valószínűségi változót is: tegyük fel, hogy ketten játszanak. Fej esetén az első játékos nyer 5 Ft-ot, írás esetén a második. Ekkor ha X jelöli az első játékos "nyereségét", akkor az így definiált valószínűségi változónak a következő két értéke van: X(F)=5, X(I)=-5.
3. Kockadobás. W ={1,2,3,4,5,6}. Legyen az X valószínűségi változó értéke a dobott szám.
3. Dobjunk fel két kockát. W most az 1 és 6 közé eső számokból álló összes lehetséges számpár. Legyen az X valószínűségi változó értéke a két dobott szám összege: X((i,j))=i+j (i,j=1,2,3,4,5,6). Az 1.táblázat mutatja a lehetséges elemi eseményeket és a hozzájuk rendelt számértékeket.
|
j=1 |
j=2 |
j=3 |
j=4 |
j=5 |
j=6 |
|
|
i=1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
(1,5) |
(1,6) |
|
X |
2 |
3 |
4 |
5 |
6 |
7 |
|
i=2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
(2,5) |
(2,6) |
|
X |
3 |
4 |
5 |
6 |
7 |
8 |
|
i=3 |
(3,1) |
(3,2) |
(3,3) |
(3,4) |
(3,5) |
(3,6) |
|
X |
4 |
5 |
6 |
7 |
8 |
9 |
|
i=4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
(4,5) |
(4,6) |
|
X |
5 |
6 |
7 |
8 |
9 |
10 |
|
i=5 |
(5,1) |
(5,2) |
(5,3) |
(5,4) |
(5,5) |
(5,6) |
|
X |
6 |
7 |
8 |
9 |
10 |
11 |
|
i=6 |
(6,1) |
(6,2) |
(6,3) |
(6,4) |
(6,5) |
(6,6) |
|
X |
7 |
8 |
9 |
10 |
11 |
12 |
1.táblázat.
4. A kísérlet egerek testsúlyának a mérése, egy elemi esemény egy állat kiválasztása véletlenszerűen, a valószínűségi változó az egér súlya.
5. Általában, minden mérés eredménye többé-kevésbé véletlenszerű ingadozást mutat, amely tehát egy vagy több valószínűségi változóval írható le. Így egy kísérleti állatot jellemző értékek, mint a testsúly, testmagasság, hőmérséklet, stb. mind valószínűségi változók.
A valószínűségi változók lehetnek
diszkrétek, folytonosak vagy kevertek. Egy valószínűségi változót diszkrétnek nevezünk, ha értékkészlete véges (vagy megszámlálhatóan végtelen).Például, az 1,2,3. példákban szereplő változók diszkrétek, a 4,5-beliek pedig folytonosak voltak.
Egy valószínűségi változót folytonosnak nevezünk, ha érékkészlete a valós számok halmaza vagy annak részhalmaza. Kevert valószínűségi változóval nem foglalkozunk.
Az eloszlásfüggvény és a sűrűségfüggvény
Diszkrét valószínűségi változók eloszlása.
Jelöljük egy X valószínűségi változó lehetséges értékeit ![]() .-nel. Ekkor ki lehet számítani a P(X=xi), i=1,2,....n valószínűségeket. Ezeknek a valószínűségeknek a sorozatát a valószínűségi változó eloszlásának nevezzük.
.-nel. Ekkor ki lehet számítani a P(X=xi), i=1,2,....n valószínűségeket. Ezeknek a valószínűségeknek a sorozatát a valószínűségi változó eloszlásának nevezzük.
Ezeknek a valószínűségeknek az alapján kiszámítható annak az eseménynek a valószínűsége, hogy az X értéke egy adott x számnál kisebb, azaz P(X<x).
Definíció.
Tekintsük az X valószínűségi változót és egy x tetszőleges valós számot
(-¥ és ¥ között) és vizsgáljuk az (X<x) esemény valószínűségét. Ezt a valószínűséget (amely x függvénye) az X valószínűségi változó (kumulatív) eloszlásfüggvényének nevezzük és F(x)-szel jelöljük:F(x)=P(X<x).n
1. példa. Legyen X a kockadobás eredménye, lehetséges értékei 1,2,3,4,5,6. Számítsuk ki a P(X=xi), xi=1,2,3,4,5,6 .valószínűségeket!
P(X=1)=P(X=2)=P(X=3)=P(X=4)=P(X=5)=P(X=6)=1/6. Ez a sorozat adja X eloszlását.
Most számítsuk ki annak valószínűségét, hogy X<x, ahol x tetszőleges valós szám. Ezt az előző valószínűségek sorozatos összegezésével kapjuk:
P(X<1)=0 , mert lehetetlen 1-nél kevesebbet dobni.
P(X<2)=1/6, mert 2-nél kevesebbet egyféleképpen dobhatunk, csak az 1-es dobás a kedvező. Ennek valószínűsége 1/6.
P(X<3)=2/6=1/3 , mert az (X<3) esemény azt jelenti, hogy (X=1) vagy (X=2).
P(X<4)=3/6=1/2)
P(X<5)=4/6=2/3
P(X<6)=5/6
P(X<6.1)=6/6=1
P(X<7)=6/6=1 és így tovább. A 2. ábra mutatja ennek az eloszlásfüggvénynek a grafikonját.
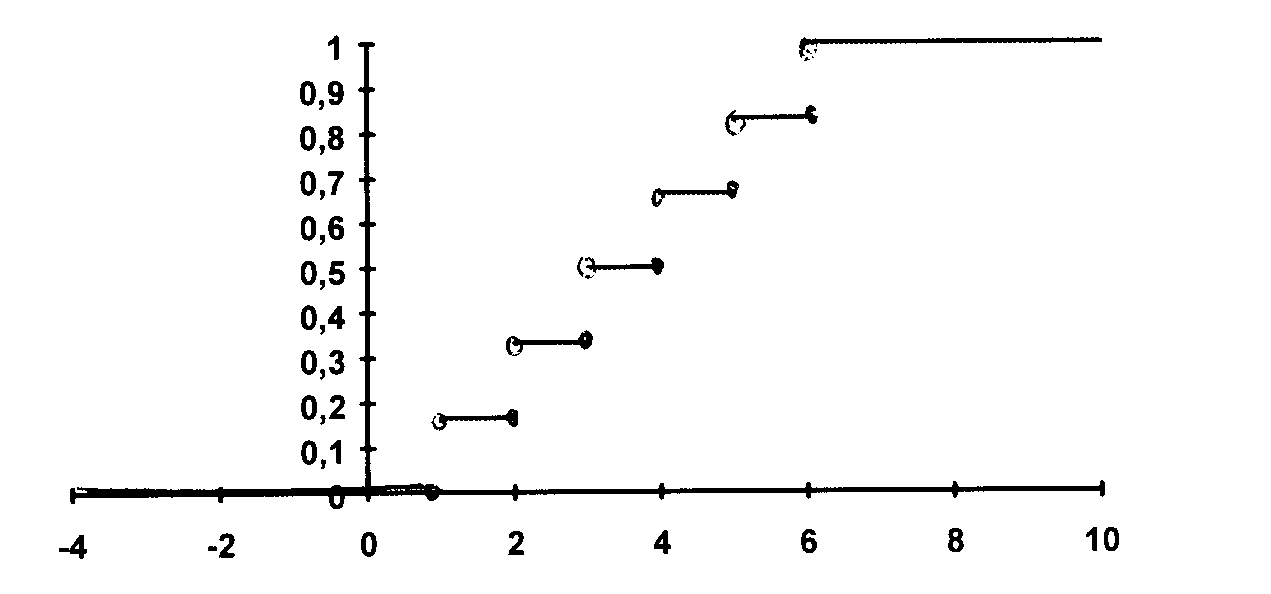
2. ábra
2. példa. Legyen a kísérlet két kockával való dobás, X legyen a két dobás számértékének összege.( Az elemi események és az X valószínűségi változó értékei az 1. táblázatbeliek, X((i,j))=i+j (i,j=1,2,3,4,5,6).) Most,
P(X=1)=0, (X=1 lehetetlen)
P(X=2)=1/36 (az egyetlen kedvező esemény az (1,1), és az összes lehetséges eset száma 36. )
P(X=3)=2/36 (a kedvező események (1,2) és (2,1) )
...
P(X=12)=1/36
Ezeknek a valószínűségeknek a rajza (X eloszlása ) a 3. ábrán látható..
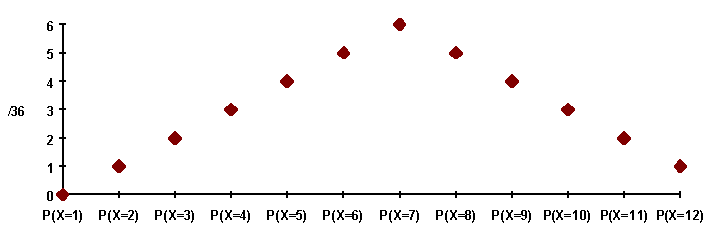
3. ábra.
Hogy X eloszlásfüggvényét megkapjuk, szükségünk van a P(X<x) valószínűségekre:
P(X<2)=0 mert az X<2 esemény lehetetlen esemény
P(X<2.1)=1/36
P(X<3)=1/36
P(X<4)=3/36 (kedvező események: (1,1) , (1,2), (2,1) )
P(X<5)=6/36 (kedvező események: (1,1) , (1,2), (2,1), (1,3),(3,1),(2,2)
...
P(X<12)=35/36
P(X<13)=1
A 4. ábra mutatja az X változó eloszlásfüggvényét. Látható, hogy ez nem folytonos,. minden egyes ugrásnál szakadása van.
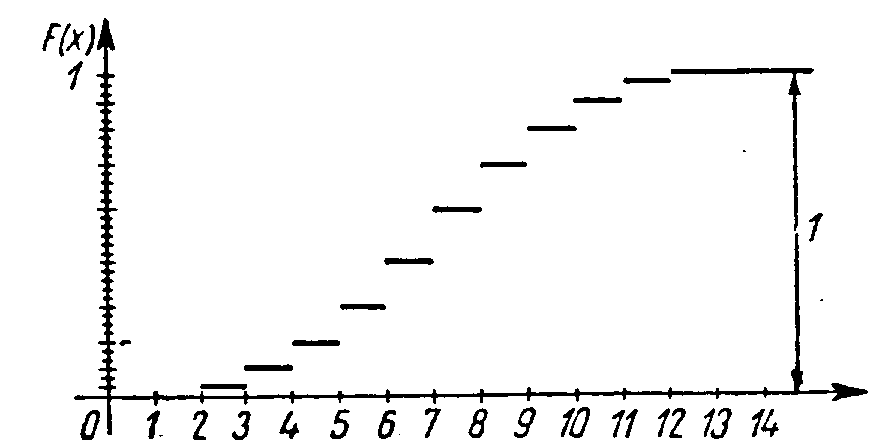
4. ábra.
Folytonos valószínűségi változó eloszlá
saHa X folytonos valószínűségi változó esetén az eloszlásfüggvény azaz F(x)=P(X<x) meghatározásához a diszkrét esetben mutatott eljárás nem alkalmazható. Tekintsük a következő példát. Legyen X egy óra mutatójának a helyzete fokokban mérve, tetszőleges időp
illanatban. X 0° és 360° között bármely értéket felvehet. Nyilván P(X<0)=0, P(X<361)=1, és a többi valószínűség az 5. ábráról olvasható le.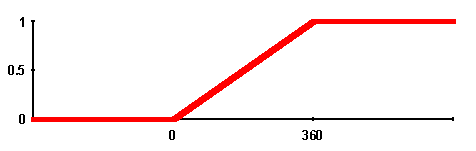
5. ábra.
Az eloszlásfüggvény tulajdonságai
Mind diszkrét, mind folytonos esetben érvényesek a következő tulajdonságok:
1. F(x) mindig monoton növekvő függvény.
2. F(x) határértéke mínusz végtelenben 0, és plusz végtelenben 1:
![]()
3. F(x) balról folytonos.
Egy folytonos valószínűségi változó sűrűségfüggvénye.
Számítsuk ki annak valószínűségét, hogy egy valószínűségi változó egy adott (a,b) intervallumba esik! Ezt a valószínűséget az F(x) eloszlásfüggvény segítségével könnyen kiszámíthatjuk.Nyilván
P(X<a)+P(a£ X<b)=P(X<b).
A második tagot kifejezve kapjuk a keresett valószínűséget
P(a£ X<b)=P(X<b)-P(X<a)=F(b)-F(a)
Ennek a valószínűségnek az alapján megadható a folytonos valószínűségi változó definíciója:
Definícó.
Az X valószínűségi változót folytonosnak nevezzük, ha létezik egy f(x)³
0 függvény, melyre|
P(a£
X<b)=F(b)-F(a)= |
(1.4) |
f(x)-et az X valószínűségi változó sűrűségfüggvényének nevezzük.n
Következmények: f(x) a F(x) függvény deriváltja: f(x)=F'(x).
F(x) és f(x) folytonos függvények. Ha az a= -¥ és b=x helyettesítéseket elvégezzük, az F(x) eloszlásfüggvényre a következő formulát kapjuk:
F(x)=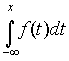 .
.
Annak valószínűsége, hogy egy folytonos valószínűségi változó egy (a,b) intervallumba esik, egyenlő az f(x) alatti területtel az (a,b) intervallum f
elett.A sűrűségfüggvénynek a következő tulajdonságai vannak:
1. f(x) nem-negatív
2. 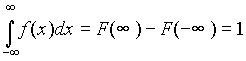 , ahol
, ahol
![]()
Példa. Legyen X ismét egy óra mutatójának a helyzete fokokban mérve, tetszőleges időpillanatban. A sűrűségfüggvénye a 4. ábrán látható függvény deriváltja. a (0,360) intervallum felett konstans (1/360), másutt 0. (6. ábra.)
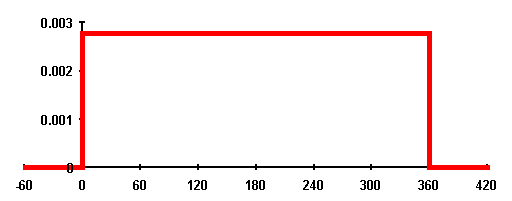
6. ábra.
A hisztogram
Az (1.4) alatti formulát heurisztikus úton is megkaphatjuk. Tegyük fel, hogy egy X folytonos valószínűségi változónak van minimuma és maximuma, melyet m ill. M jelöl. Osszuk fel a (m, M) intervallumot r egyenlő részre, így r számú részintervallumot kapunk. Egy intervallum hosszát jelöljük h-val, tehát h=(M-m)/r. Ismételjük meg az X-szel kapcsolatos kísérletet n-szer! Számoljuk meg, hogy a kapott értékekből mennyi esik egy-egy részintervallumba! Az i-edik részintervallumba eső értékek számát jelöljük ki-vel, ez annak az eseménynek a gyakorisága, hogy a kísérlet eredménye az i-edik intervallumba esik (i=1,...r). Rajzoljunk ki magasságú téglalapokat az intervallumok fölé! (5. a . ábra). A kapott ábra az adatok eloszlásáról nyújt képet. Egy intervallumba esés arányát az összes értékhez képest az adott téglalap területe mutatja. Egy téglalap területe kih, a téglalapok összterülete k1h + k2h +...+ krh =( k1+ k2+...+ kr)h=nh.
Alakítsuk úgy a téglalapok magasságát, hogy az összterület éppen 1 legyen! Ez elérhető pl. úgy, hogy gyakoriságok helyett rajzoljunk k
i/(nh) magasságú téglalapokat az intervallumok fölé. Ha a beosztás éppen 1-esével történik(h=1), akkor a téglalpok magasságai éppen a ki/n relatív gyakoriságok. A relatív gyakoriságok az adott intervallumba esés valószínűségeit közelítik. Ha a beosztás nem 1-esével történik, akkor is az adott téglalap területe közelíti az adott intervallumba esés valószínűsűgét.A téglalapok felső oldalai tehát egy sűrűségfüggvény geometriai képe, mely az f(x) elméleti sűrűségfüggvény közelítésének tekinthető. Ezt a grafikont
hisztogramnak nevezzük.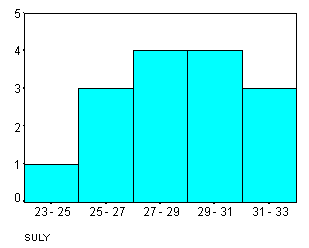
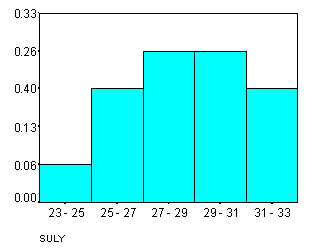
7. ábra. a) gyakoriság , b) relatív gyakoriság
A hisztogramot szokták empirikus sűrűségfüggvénynek is nevezni.
Példa: 15 egeret megmérve a következő, grammokban kifejezett súlyokat kapták: 28 31 26 26 29 31 30 27 25 30 28 28 23 32 30. Ez a sorozat a súlymérés kísérletnek 15-szöri ismétlése. Az X változó a testsúly, amelyről készült mérések eredményei most 22 és 3
2 közé esnek. Legyen r=5, ekkor h72, és a 7. ábrán látható hisztogramot kapjuk A 7.a) ábrán a téglalap magasságai gyakoriságok, a 7.b) ábrán pedig relatív gyakoriságok. Látható, hogy a két ábra csak a függőleges tengely beosztásában különbötózik. A 7.b. ábra akkor lenne tekinthető sűrűségfüggvény-közelítésnek, ha még az intervallum hosszával, 2-vel is osztanánk a magasságot.