- ...távozik
- Feltételezzük, hogy az egyéb
hőcsere-lehetőségektől (mint pl. a hőkisugárzástól)
eltekinthetünk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...szám.
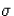 és
és 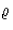 mindegyike függhetne t-től
is, de ezzel a - gyakorlati feladatokban ritkán írható -
feltétellel nem bonyolítjuk tovább a levezetést.
mindegyike függhetne t-től
is, de ezzel a - gyakorlati feladatokban ritkán írható -
feltétellel nem bonyolítjuk tovább a levezetést.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...0.
- Érvényes ugyanis az alábbi állítás: ha az f
folytonos függvény értelmezési tartománya egy I intervallum és minden
![$[a,b]\subset I$](img42.gif) -re
-re 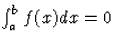 , akkor
, akkor 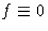 I-n.
Valóban,
tekintsük az
I-n.
Valóban,
tekintsük az 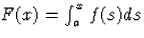 függvényt, ahol
függvényt, ahol 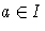 tetszőleges,
rögzített szám. f folytonossága miatt F deriválható és
tetszőleges,
rögzített szám. f folytonossága miatt F deriválható és
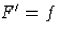 , másrészt a feltétel szerint F(x)=0 minden
, másrészt a feltétel szerint F(x)=0 minden 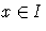 -re. Azaz
f az I-n azonosan 0 függvény deriváltja, amiből állításunk
következik.
-re. Azaz
f az I-n azonosan 0 függvény deriváltja, amiből állításunk
következik.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...rúdra.
- Ettől eltérő pontokban
megadott feltételekkel a feladat lényegesen bonyolultabbá válik.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...környezetében
- Egy pont környezetein a pontot tartalmazó nyílt
intervallumokat értjük.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...nélkül
- A
bizonyítások megtalálhatók pl. az [3] könyvben.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...láncszabályt.
- A láncszabály
kettőnél több változójú függvényekre is kimondható.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...legyen!
- Ezzel tulajdonképpen ahhoz a kérdéshez
térünk vissza, hogy hogyan kell a g és h függvényeket megválasztani
f-hez, amikor a (57)-ról áttérünk a (58) egyenlet
re.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...feltételek
- Ezek: g és h legyen
folytonosan deriválható, továbbá
e két függvénynek ne legyen azonos pontban zérushelye.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...jelölést
- Vegyük észre, hogy (58) egzaktságát éppen az dönti el,
hogy r=0 vagy sem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...függvény
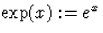
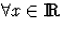 .
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...kombinációjaként.
- Ezt a két állítást
együtt úgy is szokták mondani, hogy a síkbeli vektorok 2
dimenziós vektorteret alkotnak.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...segítségével
- Az is előfordulhat, hogy a differenciálegyenlet megoldását képlet írja
le, mi
ezt a képletet ismerjük, de túl bonyolult, ezért egy vagy több
pontban való kiértékelése több fáradsággal, esetleg nagyobb
hibával járna, mintha egyből egy közelítő eljárással
számolnánk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...környezetében
- Ez azt jelenti, hogy az n-edik
rendig bezárólag az összes parciális deriváltja létezik és
folytonos az (x0,y0) pont környezetében.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...láncszabályt
- Lásd a 2.5. alfejezetet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...nélkül
- A bizonyítás megtalálható
pl. [4]-ban.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.