Igazold, hogy a fenti négy pont nincs egy síkon és számítsd ki az általuk meghatározott tetraéder térfogatát!
Határozd meg annak az egyenesnek az egyenletrendszerét, amely átmegy a D ponton, mer˘leges az
Határozd meg D távolságát az
Add meg annak az S síknak az egyenletét, amely tartalmazza e-t és mer˘leges
Bizonyítsd be, hogy a fenti négy pont tetraédert határoz meg, majd számítsd ki az AD él és az
Add meg annak az S síknak az egyenletét, amely párhuzamos e-vel és tartalmazza A-t és B-t is!
Bizonyítsd be, hogy a fenti három pont nincs egy egyenesen és számítsd ki az általuk meghatározott háromszög területét!
-
Írd fel a P-n átmen˘,
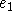 -gyel párhuzamos egyenes paraméteres
egyenletrendszerét!
-gyel párhuzamos egyenes paraméteres
egyenletrendszerét! -
Milyen messze van P attól az S síktól, amely mer˘leges
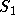 -re
és tartalmazza
-re
és tartalmazza 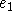 -et!
-et!
- Írd fel az A pontra és az x-tengelyre illeszked˘ sík egyenletét!
- Milyen messze van B a fenti síktól?
- Bizonyítsd be, hogy a két egyenes metszi egymást és írd fel a mindkett˘re illeszked˘ sík egyenletét!
- Mekkora szögben metszi ez a sík a z-tengelyt?
-
Írd fel
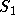 és
és 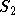 metszésvonalának egyenletét!
metszésvonalának egyenletét! - Milyen messze van az origó a metszésvonaltól?
-
Írd fel annak az S síknak az egyenletét, amely mer˘leges
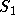 -re és
-re és 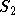 -re is és átmegy az origón!
-re is és átmegy az origón! - Milyen messze van a P(1,2,3) pont S-t˘l?
-
Bizonyítsd be, hogy P rajta van S-en és
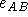 párhuzamos
S-sel!
párhuzamos
S-sel! -
Írd fel annak a P-n átmen˘, S-ben haladó e egyenes
paraméteres egyenletrendszerét, amely mer˘leges
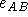 -re!
-re! - Milyen messze van A e-t˘l?
- Bizonyítsd be, hogy a fenti négy pont nincs egy síkon! Mennyi az általuk meghatározott tetraéder térfogata?
-
Írd fel annak a C-n és D-n is átmen˘ S sík
egyenletét, amely párhuzamos
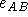 -vel!
-vel! -
Mekkora szöget zár be S és
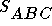 ?
?
- Számítsd ki az ABC háromszög területét és az A-nál lév˘ szögét!
- Írd fel annak az S síknak az egyenletét, amely illeszkedik
A-ra és párhuzamos
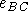 -vel és az x-tengellyel!
-vel és az x-tengellyel!