II. Valószínűségelmélet és statisztika
2.1. Populácó és minta
Az utóbbi fejezetben változók eloszlását vizsgáltuk, de azzal nem foglalkoztunk, hogy azok hogyan realizálódnak egyes esetekben. Csak azt állapítottuk meg, hogy egy X valószínűségi változó milyen valószínűséggel esik egy adott intervallumba. Ez a valószínűség bizonyos paraméterektől függ, amelyek ezt az általában ismeretlen eloszlást leírják. Tehát nincs semmi ismeretünk az eloszlásról, ezt kísérleti úton nyert tapasztalati eloszlással kell közelítenünk. Kísérleteket végzünk e célból, amelynek az eredménye véges számú mérési eredmény, ún. statisztikai minta lesz.
A statisztikai vizsgálat tárgyát képező egyedek összességét a megfelelő számértékekkel együtt
statisztikai sokaságnak vagy populációnak nevezzük. Más szóval, a populáció azoknak az elemeknek, objektumoknak az összessége, amelyről információt kívánunk nyerni.Ha egy populáció véges számú elemet tartalmaz, akkor véges populációról beszélünk. Elméletileg, idealizált esetben elképzelhető végtelen populáció is.
A populáció elemeinek általában valamilyen numerikus jellemzőit vizsgáljuk, minden elemhez a vizsgálatra jellemző szám rendelhető. Ezt a tulajdonságot egy valószínűségi változóval fejezhetjük ki, azaz, a populáció egy X valószínűségi változóval hozható kapcsoltaba. X eloszlását a populáció eloszlásának nevezzük.
1.Példa. Magyarország lakói véges populációt képeznek. A numerikus jellemző (valószínűségi változó) lehet például egy lakos évi jövedelme forintban.
2.Példa. A gyógyszerészhallgatók halmaza is egy populáció, a numerikus jellemző a hallgatók testmagassága.
3.Példa. Tegyük fel, hogy egy kutató az egyéves hímnyulak átlagos súlyát szeretné meghatározni. Lehetetlen a populáció összes egyéves hímnyulát megmérni, mivel a populáció sosem létezik teljes egészében egy adott időpontban. Ha a kutató pld. 50 darab hímnyulat véletlenszerűen kiválaszt, ez az 50 nyúl lesz az alapja a populáció vizsgálatához. Ez az 50 nyúl ún. statisztikai mintát képez.
Ismételjünk meg egy kísérletet n-szer, a populáció n elemén. Így n számú megfigyelést kapunk. Az ismétléseket egymástól függetlenül, ugyanazon körülmények között kell végrehajtanunk. Minden ismétlés eredménye egy valós szám lesz, amely egyúttal egy X valószínűségi változó értéke. Jelöljük az így kapott számsorozatot ![]() -nel.
-nel.
Definícó.
Az egymástól független és X-szel megegyező eloszlású
A mintaelemeknek egy populációból történő véletlenszerű kiválasztásának több módszere is van (visszatevés nélkül, visszatevéssel, szekvenciálisan, stb.). A véletlen mintában a kiválasztás azon elv szerint történik, hogy a populációnak minden eleme egyforma valószínűséggel legyen választható. A mintavételezés
a biostatisztika egyik fontos kérdése, de mi nem foglalkozunk vele.2. Példa. Az összes gyógyszerészhalgatók populációjában 10 véletlenszerűen választott hallgató 10 elemű mintának tekinthető.
A statisztikai vizsgálat célja egyrészt populációról a minta alapján leíró információkat szerezni, másrészt következtetéseket szeretnénk levonni, hipotéziseket bebizonyítani. Az első cél a leíró statisztika, a második pedig a statisztikai analízis, következtetés témaköre. A következő fejezetben a leíró statisztika módszereivel foglalkozunk, azaz, a minta alapján a populáció jellemzésével.
2.2. Populácó- és mintabeli jellemzők
2.2.1. A populáció és a minta eloszlása
Tekintsünk egy ![]() statisztikai mintát, mely az F(x) eloszlású populációból származik. Ez egyúttal az X valószínűségi változó eloszlásfüggvénye is, melyet tehát a populáció eloszlásfüggvényének vagy elméleti eloszlásfüggvénynek nevezünk. Hasonlóan (folytonos esetben) f(x) az elméleti sűrűségfüggvény, mindkettő többnyire ismeretlen.
statisztikai mintát, mely az F(x) eloszlású populációból származik. Ez egyúttal az X valószínűségi változó eloszlásfüggvénye is, melyet tehát a populáció eloszlásfüggvényének vagy elméleti eloszlásfüggvénynek nevezünk. Hasonlóan (folytonos esetben) f(x) az elméleti sűrűségfüggvény, mindkettő többnyire ismeretlen.
Az ![]() értékek a számegyenesen véletlenszerűen helyezkednek el, minden konkrét esetben azonban kapunk n meghatározott pontot. Ha az így kapott pontok mindegyikéhez hozzárendelünk 1/n valószínűséget, akkor egy diszkrét valószínűségeloszlást kapunk, melyet empírikus eloszlásnak nevezünk, az ehhez tartozó eloszlásfüggvényt a minta eloszlásfüggvényének vagy empírikus eloszlásfüggvénynek nevezzük. Minél nagyobb az n, annál jobban megközelíti a minta eloszlásfüggvénye az elméleti eloszlásfüggvényt.
értékek a számegyenesen véletlenszerűen helyezkednek el, minden konkrét esetben azonban kapunk n meghatározott pontot. Ha az így kapott pontok mindegyikéhez hozzárendelünk 1/n valószínűséget, akkor egy diszkrét valószínűségeloszlást kapunk, melyet empírikus eloszlásnak nevezünk, az ehhez tartozó eloszlásfüggvényt a minta eloszlásfüggvényének vagy empírikus eloszlásfüggvénynek nevezzük. Minél nagyobb az n, annál jobban megközelíti a minta eloszlásfüggvénye az elméleti eloszlásfüggvényt.
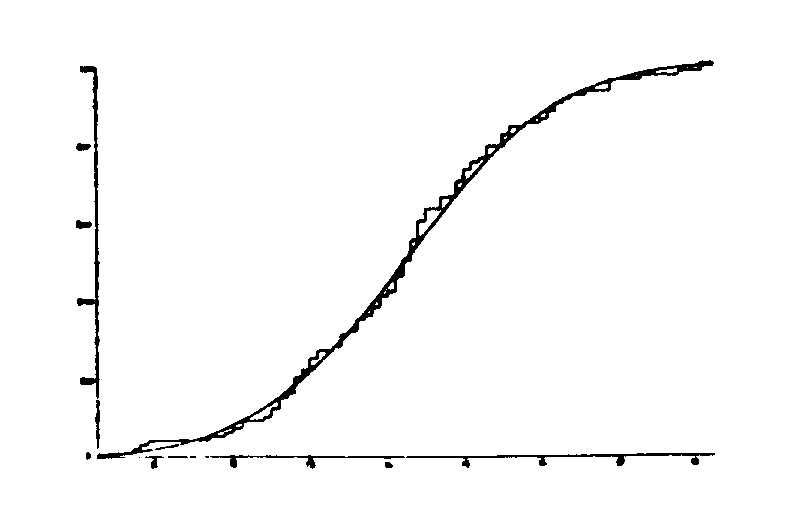
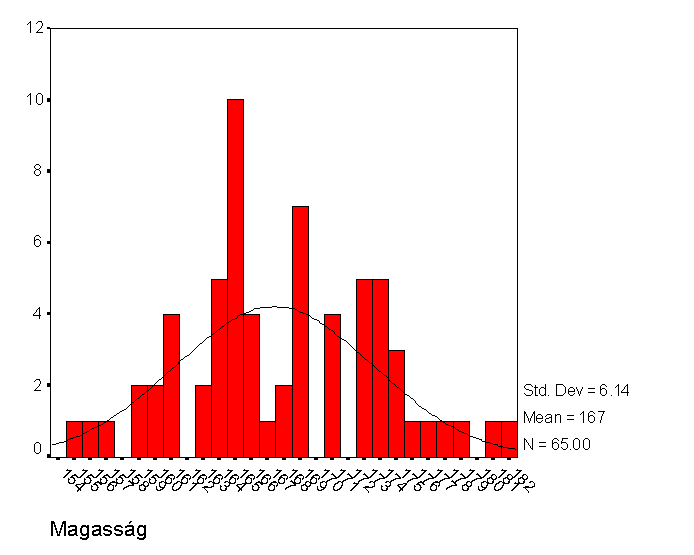
Hasonlóan nyerhető folytonos eloszlás esetén a minta sűrűségfüggvénye. Az előző fejezetben látott hisztogram is az elméleti sűrűségfüggvény egy közelítése.A 8.a-b ábra mutat egy példát a minta és a populáció eloszlás- és sűrűségfüggvényére.
|
8.a.ábra. Folytonos eloszlásfüggvény és közelítése empírikus sűrűségfüggvénnyel |
8.b.ábra. Folytonos sűrűségfüggvény és közelítése empírikus sűrűségfüggvénnyel. |
2.2.2. A centrális tendencia mérőszámai
A kutató gyakran keres olyan számokat, amelyek az adatai általános jellemvonását tükrözik. Ilyen jellemzők az átlag, a módusz és a medián, melyeket a következőképpen definiálunk:
Tekintsük az ![]() mintát.
mintát.
Az átlag vagy mintabeli átlag a mintaelemek számtani közepe, azaz:
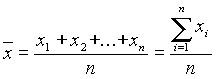 (2.1)
(2.1)
A módusz a minta leggyakrabban előforduló eleme.
A medián az az érték, amelynél a mintaelemek fele kisebb, és amelynél a mintaelemek fele nagyobb. Kiszámítása oly módon történik a mintaelemekből, hogy a mintát először nagyság szerint rendezzük, és páratlan mintaelemszám esetén a középső elem a medián, páros mintaelemszám esetén a két középső elem számtani közepe.
1.Példa. 11 hallgató maximum 100 pontos teszteredményei a következők: 100 100 100 63 62 60 12 12 6 2 0. Az átlag 517/11=47, a modus 100, a medián 60. Az egyik hallgató szerint szigorú volt a tanár, mert a 47-es átlagot alacsonynak találta. A tanár szerint több 100 pontos teszt volt, mint bármely más teszt. Végül a tanszékvezető megfelelőnek találta az eredményeket, mivel a közepes érték, 60 nem mondható rendkívülinek.
Kinek volt igaza? Mindhárman szerették volna az adatokat legjobban jellemző egyetlen számot megadni. A hallgató az átlagot, a tanár a móduszt, a tanszékvezető a mediánt használta.
2. Példa. Számítsuk ki a 3,7,5,6,8 minta mediánját.Átrendezés után kapjuk a 3,5,6,7,8 sorrendet, a medián a középső elem, 6. A 3,3,5,6,8,13 minta mediánja viszont (5+6)/2=5.5.
Melyik a jobb a három mérőszám közül? Ez az adott helyzettől függ. Például, az átlagot egy-két szélsőséges mintaelem nagyon "elhúzza", míg a medián kevésbé függ a mintából feltűnően "kilógó", extrém nagy vagy kicsi értékektől.
A mintabeli jellemzők kapcsolata a populációbeli jellemzőkkel
Hasonlóan az elméleti és tapasztalati eloszlások közötti kapcsolathoz, amely a populáció és a minta közötti kapcsolatra vezethető vissza, a minta átlagának, móduszának és mediánjának is megvan az elméleti "megfelelője": az elméleti átlag, módusz, valamint a medián.
A minta átlag a populáció átlagnak vagy elméleti átlagnak vagy a várható értéknek a közelítése. A populáció átlagát a m görög betűvel jelöljük, és ez az összes populációbeli elem összege osztva az elemek számával. A minta módusza az elméleti eloszlás helyi maximumának egy közelítése, a minta mediánja a populáció mediánjának egy közelítése.
Az átlag tulajdonságai
1. Ha a mintaelemekhez ugyanazt a számot adjuk hozzá, akkor az így számolt mintaátlag is ugyanezzel a számmal tér el az eredetitől. Ugyanez érvényes egy szám kivonására, számmal való szorzásra és osztásra.
2. Az átlag az a szám, amelynek a négyzetes eltérése a mintaelemektől minimális.
Ezt a második állítást a differenciálszámítás eszközeivel be lehet bizonyítani. Jelölje m azt a számot, amelynek a mintaelemektől való négyzetes eltérését vizsgáljuk. Ez a négyzetes eltérés adott mintaelemek esetén m függvénye, tehát a következő függvény minimumát keressük:
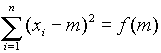 .
.
A szélsőértékek megkereséséhez a fenti függvényt kell
m szerint differenciálnunk: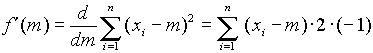
Tegyük egyenlővé a jobboldalt 0-val, és oldjuk meg az egyenletet
m-re:![]()
Az utolsó egyenlőségből
m -et kifejezve kapjuk a (2.1) alatti formulát: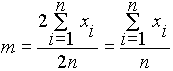
Tehát a számtani átlag szélsőérték hely. Bebizonyítható, hogy e
z minimum is, mert a második derivált mindig pozitív: 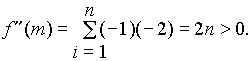
2.2.3. A szóródás mérőszámai
Szükségünk van egy olyan mérőszámra is, amely azt mondja meg, hogy a mintaelemek közel vannak-e az átlagtól, vagy távol vannak tőle. Egy ilyen mérőszámot a szóródás mérőszámának nevezzük, ideális esetben ez a szám akkor nagy, ha a mintaelemek távol vannak az átlagtól, és kicsi, ha közel. Ilyen, a leggyakrabban alkalmazott mérőszámok a terjedelem, a variancia és a standard deviáció.
A minta terjedelme
A terjedelem a minta legnagyobb eleme (maximuma) és legkisebb eleme(minimuma) közötti különbség.
A variancia
Most tekintsünk egy, az átlagtól való eltérést mérő számot. Az átlagtól egyenlő távolságra levő egyedek egyenlő mértékben járulnak hozzá ehhez a számhoz, akár pozitív, akár negatív az átlagtól való eltérésük. Négyzetre emeléssel eltüntethető a negatív elő
jel, tehát definiáljuk a minta szóródását az átlagtól való átlagos négyzetes eltéréssel, amit varianciának nevezünk. A variancia képlete a következő:|
|
(2.2) |
A standard deviáció
Mivel a varianciát gyakran nehéz elképzelni, általánosabban használt mérőszám a szóródásra a variancia négyzetgyöke, amit
standard deviációnak vagy a minta szórásának nevezünk. A standard deviáció képlete:|
|
(2.3) |
A standard deviációnak ugyanaz a (fizikai) mértékegysége, mint az átlagé, ill. az eredeti adatoké. Gyakorlatban, kézi számoláshoz megfelelőbbek a standard deviáció következő, átalakított formái:
|
|
(2.4) |
A populációbeli szóródás mérőszámai
A szóródás mérőszámai is definiálhatók a teljes populációra is, így a minta terjedelme, varianciája és standard deviációja a populáció terjedelmének, varianciájának és standard deviációjának közelítései.
Példa. Számoljuk ki az 1, 8, 0, 3, 9 standard deviációját a (2.3) és a (2.4)-beli képlet segítségével. Látható, hogy egyszerűbb a (2.4)-ben megadott képlet használata.
|
i |
xi |
xi-4.2 |
(xi-4.2)2 |
xi |
xi2 |
||
|
1 |
1 |
-3.2 |
10.24 |
1 |
1 |
||
|
2 |
8 |
3.8 |
14.44 |
8 |
64 |
||
|
3 |
0 |
-4.2 |
17.64 |
0 |
0 |
||
|
4 |
3 |
-1.2 |
1.44 |
3 |
9 |
||
|
5 |
9 |
4.8 |
23.04 |
9 |
81 |
||
|
S |
S xi=21 |
S
(xi-4.2)2= |
S xi=21 |
S
xi2= |
|||
|
|
|
||||||
|
|
|||||||
|
|
|||||||
A standard deviáció tulajdonságai
1. Ha a mintaelemekhez ugyanazt a számot hozzáadjuk, vagy a mintaelemekből ugyanazt a számot levonjuk, az így keletkezett minta szórása mege
gyezik az eredeti minta szórásával.2. Ha a mintaelemeket ugyanazzal a számmal szorozzuk, az így keletkezett minta szórása az eredeti minta szórásának konstansszorosa lesz. Ugyanez érvényes egy konstanssal való osztásra is.
2.2.4. Egy mintaelem mérőszáma a mintában vagy a populációban
z érték, vagy standardizált érték
Egy mintaelemre vonatkozó mérőszám természetesen adódik: maga a mérés eredménye, az a szám, amelyet a mintavételezés során kapunk. Egy másik fontos mérőszáma egy mintaelemnek az ún. z érték,
vagy a mintaelem standardizáltja. A z érték megadja, hogy a mintaelem eltérése a minta átlagától a standard deviáció hányszorosa. Ha adott egy minta, az xi mintaelemhez tartozó z érték a következőképpen számítható :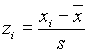 , i=1,2,...,n.
, i=1,2,...,n.
Példa . Egy osztályban egy tesztnek a következő eredményei születtek: az átlag 83 pont volt, a standard deviáció 5, a medián 87 és a terjedelem 24. Az egyik gyereknek ebben az osztályban 69 pontos eredménye lett. Az ehhez tartozó z érték
z=(69-83)/5=-14/5=-2.8. Ez azt mutatja, hogy ennek a gyereknek a teljesítménye majdnem 3 standard deviációval volt az átlag alatt.A z értéket a mintaelemek relatív helyzetének a jellemzésére is használhatjuk. Tekintsünk két vizsgaeredményt, melyet egy hallgató elért: angolból 85 pont, fizikából 65. Tegyük fel, hogy az angol tesztek átlaga 70 lett, a fizika teszteké pedig 50. Azt jelenti-e ez, hogy a hallgató relatíve ugyanazt az eredményt érte el mindkét tárgyból? (az átlagtól való eltérés 15 mindkét esetben). Ha figyelembe vesszük a szórásokat is, és kiszámítjuk a z értékeket, láthatjuk, hogy nem, az átlagtól való eltérés önmagában nem elegendő a hallgató mintabeli relatív helyzetének a meghatározásához, amint ezt a következő táblázat is mutatja:
|
Angol |
Fizika |
||
|
100 |
65 |
a hallgató pontszáma |
|
|
99 |
57 |
||
|
98 |
55 |
||
|
85 |
a hallgató pontszáma |
53 |
|
|
73 |
50 |
||
|
67 |
49 |
||
|
60 |
47 |
||
|
53 |
44 |
||
|
45 |
44 |
||
|
20 |
36 |
||
|
|
|
||
|
s=26.4 |
s=8.1 |
Ebből a táblázatból látható, hogy bár az átlagtól
való eltérés mindkét esetben ugyanannyi, a hallgató fizikából relatíve jobb volt, mint angolból. Hogy lássuk, hogyan viszonyul a hallgató a többihez, számítsuk ki a z értékeket. A hallgató angol tesztjének z értéke z=(85-70)/26.4=15/26.4=0.56, a fizikáé z=(65-50)/8.1=15/8.1=1.9. Látható, hogy a fizika eredmény relatíve jobb.
Rangsorolás
Másik lehetséges mérőszám egy mintaelem pozíciójának a meghatározására a mintaelemnek a rendezett mintában elfoglalt helye (pld. "10-ből a negyedik") . Ez főként kis mintae
lemszám esetén használható.Feladatok.
1. 20 ember vérnyomását mérték és csak azt figyelték, hogy a vérnyomás alacsony (A), normál (N), vagy magas (M) tartományba esik-e. A következő mintát kapták:
M,M,N,M,M,N,A,A,N,N,N,N,M,M,N,N,M,M,A,N.
Készítsünk relatív gyakorisági hisztogramot a mintából, és interpretáljuk az eredményt.
2. Számítsuk ki a következő minták átlagát, standard deviációját, mediánját és terjedelmét. Ahol szükséges, alkalmazzunk transzformációt.
a) -2, 0, 2, 4, 6 (n=5)
b) 2, 5, 4, 2 (n=4)
c) 3, 5, 1, 0, 3, 4 (n=6)
d) 1002, 1005, 1004, 1002 (n=4).
3. Számolás nélkül hasonlítsuk össze a következő hőmérsékletek átlagát és standard deviációját:
Kodiak, Alaska: 10, 8, 0, -1
Coldfoot, Alaska: -10, -8, 0, 1
4. Számolás nélkül hasonlítsuk össze a következő életkorok átlagát és standard deviációját:
X: 5,2,7,3
Y: 65, 62, 67, 63
5. Számítsuk ki a 2,5,6,7 elemekből álló minta átlagát és szórását! Adjuk meg az átlagtól több, mint 2-szeres standard deviáció távolságra levő mintaelemeket.
6. Adjunk meg egy ötelemű mintát, melynek a varianciája 0 .