III. Nevezetes eloszlások és tételek
3.1. A binomiális eloszlás
Tekintsünk egy kísérletet, amelynek két lehetséges kimenete van. Minden olyan kísérletet, amelyben csupán egy A esemény és ennek kiegészítője érdekel bennünket, egy ilyen, két kimenetelű kísérletnek tekinthetünk. Nyilván
![]() .
.
Jelölje a kimenetelek valószínűségeit
p és q :![]()
Végezzük el a kísérletet n-szer egymástól függetlenül. Jelölje X az A esemény gyakoriságát. Az X valószínűségi változó lehetséges értékei 0,1,...,n. Bebizonyítható, hogy annak valószínűsége, hogy X egy adott k értéket vesz fel, az alábbi formulával számítható ki:
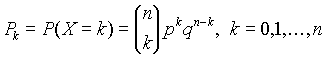 , (3.1)
, (3.1)
ahol 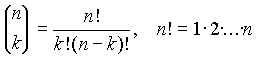 .
.
Bebizonyítható, hogy a Pk valószínűségek összege 1. Adott p és n esetén az X valószínűségi változó tehát diszkrét eloszlású. A (3.1) eloszlást binomiális eloszlásnak nevezzük n és p paraméterekkel. A 9. ábrán látható a binomiális eloszlás képe, a 9-a ábrán fix p és különböző n esetén, a 9-b ábrán fix n és különböző p esetén. Az ábrák segítenek a binomiális eloszlás és más eloszlások közötti hasonlóság felfedezésében..


9. a-b. ábra
Példa. Egy kutató mérnök bizonyos protein előállításával kísérletezik. Ismeretes genetikai meggondolások alapján, hogy egy ilyen kísérlet sikerének a valószínűsége 0.7. A kutatónak összesen a kísérlet 6-szori ismétléséhez van elegendő pénze, illetve anyaga. Számítsuk ki, hogy ebben az esetben mi a valószínűsége, hogy a 6 közül
2 kísérlet lesz sikeres.Megoldás. p=0.7, n=6. P(X=2)=15(0.7)2(0.3)4=0.06.
A következő táblázatban n=6 esetén minden lehetséges
k-ra kiszámoltuk a siker valószínűségét:|
k |
|
Pk=P(X=k) |
|
0 |
1 |
1q6=1(0.3)6=0.000729 |
|
1 |
6 |
6p1q5=6(0.7)(0.3)5=0.01 |
|
2 |
15 |
15p2q4=15(0.7)2(0.3)4=0.06 |
|
3 |
20 |
20p3q3=20(0.7)3(0.3)3=0.19 |
|
4 |
15 |
15p4q2=15(0.7)4(0.3)2=0.32 |
|
5 |
6 |
6p5q1=6(0.7)5(0.3)1=0.3 |
|
6 |
1 |
1p6=1(0.7)6=0.12 |
Esetenként a p nem ismert, a feladat éppen az ő értékének a közelítése egy minta alapján .
Ha n a végtelenbe tart, de ugyanakkor az np szorzat állandó, azaz np=l , a binomiális eloszlás egy másik diszkrét eloszlást közelít, mely a következő képlettel adható meg:
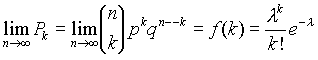 (3.2)
(3.2)
Itt f(k) képlettel megadható eloszlást Poisson eloszlásnak nevezzük l paraméterrel. Csak egész k-ra van értelmezve. A 10. ábra különböző l esetén mutatja be a Poisson eloszlást.
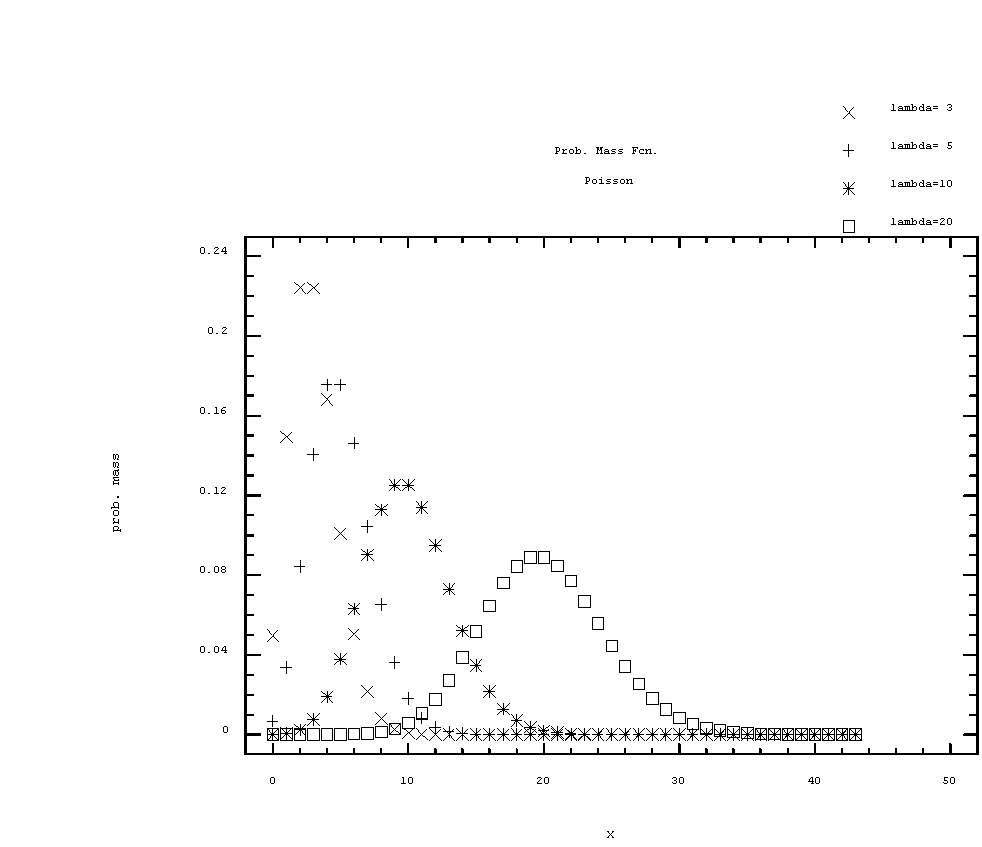
10. ábra
A Poisson eloszlást a binomiális eloszlásból nyertük nagy n, de konstans l =np esetén. Ha np konstans, p-nek kicsinek kell lennie. Tehát Poisson eloszlás olyan esetben lép fel, amikor egy esemény nagyon gyakran előfordul, de a minket érdeklő kimenetel valószínűsége, p kicsi. (Tehát nagy számú "próbálkozás" és kevés számú "siker"). Például Poisson eloszlást követ a vérsejtek száma a mikroszkóp látómezejében, a csillagok száma az égbolt bizonyos területén, egy süteményszeletben levő mazsolák száma, egy mérkőzésen a gólok száma, a lórugásokból bekövetkező halálos balesetek száma, a telefonközpontba beérkező hívások száma, radioaktív atomok száma a bomlás bizonyos stádiumában, a meteorológiai frontok érkezései, stb.
Eddig diszkrét változók eloszlásait elemeztük. Most tekintsük a folytonos változók eloszlásai közül a legegyszerűbbet, a folytonos egyenletes eloszlást. Egy X változót egyenletes eloszlásúnak nevezünk, ha sűrűségfüggvénye a következő::
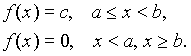 (3.3)
(3.3)
Tehát f(x) konstans az (a,b) intervallumon, egyébként pedig 0. A konstans értéke 1/(b-a) kell hogy legyen. Példa: a 11.oldalon bemutatott eloszlás (az óramutató helyzete egyenletes eloszlású).
3.4. A normális (Gauss) eloszlás
Egy folytonos valószínűségi változót normális eloszlásúnak nevezünk m
és s paraméterekkel és N(m ,s )-val jelöljük, ha a sűrűségfüggvénye a következő alakú: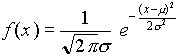 (3.4)
(3.4)
A megfelelő eloszlásfüggvény:
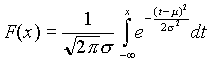 (3.5)
(3.5)
Ennek az eloszlásnak nagy jelentősége van a matematikai statisztikában, ezért tulajdonságait részletesen tárgyaljuk.
A normális eloszlás sűrűségfüggvényének tulajdonságai
A görbe szimmetrikus m -re, és ez a pont egyúttal a függvény egyetlen maximumhelye. m tehát az eloszlás átlaga, mediánja és módusza. A függvény grafikonja harang alakú. Differenciálással meggyőződhetünk róla, hogy az f(x) függvénynek két inflexiós pontja van, mégpedig a m -s és m +s helyeken.
Az eloszlás két paramétere m és s . Gyakori feltevés, hogy a mérési hibák eloszlása a m átlag körül normális eloszlás, m -t így szokás az eloszlás átlagának is nevezni. Az eloszlás s paramétere az eloszlás standard deviációja, melyet a minta standard deviációjával közelíthetünk. A két paraméternek speciális jelentése van: annak valószínűsége, hogy egy egyedi megfigyelés a valódi értéktől (az eloszlás átlagától) egyszeres standard deviációnyira tér el, 0.682 . Ez elég alacsonynak tűnik. Ezért a kutatók a standard deviáció 2- vagy 3-szorosát szokták venni, amellyel ez a valószínűség 0.954-ra illetve 0.998-ra emelkedik. Tehát annak valószínűsége, hogy egy egyedi megfigyelés a valódi értéktől (az eloszlás átlagától) kétszeres standard deviációnyira tér el, 0.954. A 11. ábra az f(x)-et mutatja, és a paraméterek jelentését.
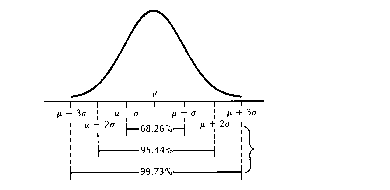
11. ábra. A normális eloszlás sűrűségfüggvénye és a paraméterek jelentése.
Speciális eset: a standard normális eloszlás
m =0 és s =1 esetén, (3.4) a következő alakú, és jelölése j (x):
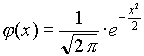 (3.6)
(3.6)
Hasonlóan (3.5) -öt F (x)-szel jelölik és a következő alakú:
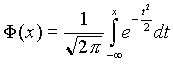
Standardizálás
Ha az X valószínűségi változó N(m
,s ) normális eloszlású , akkor a![]()
változó N(0,1) standard normális eloszlású. Ezért, ha az ![]() minta egy N(m
,s
) eloszlású populációból származik, a minta z étékei, azaz a standardizált mintaelemek standard normális eloszlásúak lesznek
minta egy N(m
,s
) eloszlású populációból származik, a minta z étékei, azaz a standardizált mintaelemek standard normális eloszlásúak lesznek
A normális eloszlás táblázata
A F (x) függvény értékei táblázatos formában általában minden statisztikával foglalkozó könyvben megtalálhatók. A 3. táblázat ezeknek egy szűk kivonatát tartzalmazza, itt minden egyes x-hez a táblázat megadja a sűrűségfüggvény alatti területet az x-től balra. Más táblázatok az eloszlás szimmetriája miatt csak pozitív x-ekre közlik a fenti értékeket, vagy nem az x-től balra, hanem jobbra eső területet vagy félterületet tartalmazzák. Sok táblázat nem az eloszlás, hanem a sűrűségfüggvény értékeit tartalmazza.
1.példa. Adjuk meg a standard normális eloszlás alatti területet az x=-1.65 és x=1 helyek között.
Megoldás. F (-1.65)=0.0495, F (1)=0.8413. A keresett területet kivonással kapjuk: 0.8413-0.0495=0.7918
2. példa. Bizonyos laboratóriumban a kísérleti patkányok testsúlyait normális eloszlásúnak találták m =14 átlaggal és s =2 szórással. Egy ilyen populációban mi annak a valószínűsége, hogy a patkányok testsúlya 10 és 15 közé esik?
Megoldás. A 13. ábra vázlatosan mutatja ezt az eloszlást. Standardizálás után a m =14-nek megfelel a z=0, A 2 standard deviációnak pedig az 1. Alkalmazzuk a z transzformációt a 15-re és a 20-ra, kapjuk a következő standardizált értékeket:
z15=(15-14)/2=0.5 and z10=(10-14)/2=-4/2=-2.
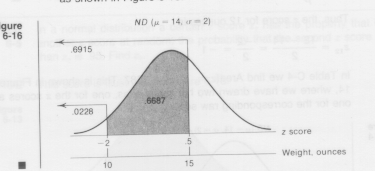
13.ábra.
F (0.5)=0.6915 és F (-2)=0.0228. Kivonás után 0.6915-0.0228=0.6687. Tehát várhatóan a populáció 67 %-ának a testsúlya fog 10 és 15 közé esni.
|
x |
F (x): x-től balra eső terület |
|
-4 |
0.0003 |
|
-3 |
0.0013 |
|
-2.58 |
0.0049 |
|
-2.33 |
0.0099 |
|
-2 |
0.0228 |
|
-1.96 |
0.0250 |
|
-1.65 |
0.0495 |
|
-1 |
0.1587 |
|
0 |
0.5 |
|
1 |
0.8413 |
|
1.65 |
0.9505 |
|
1.96 |
0.975 |
|
2 |
0.9772 |
|
2.33 |
0.9901 |
|
2.58 |
0.9951 |
|
3 |
0.9987 |
|
4 |
0.99997 |
3. Táblázat
3. Példa Frankenstein professzor vámpír denevéreket telepít a laboratóriumába. A denevérek tépőfogainak a hossza normális eloszlást követ m
=28 mm átlaggal és s =4 mm szórással. Frankenstein tudja, hogy azoknak az állatoknak a harapása halálos, akiknek a tépőfogmérete a populáció felső 5 %-ába esik. Számítsuk ki, hogy ez hány mm-es fogméretet jelent.Megoldás. A szituációt a 14.ábra szemlélteti. Mivel a 3. táblázatban az x-től balra eső területek vannak meg, az x-től jobbra eső terület nagyságát kivonással kapjuk: 1-0.05=0.95. Mivel 0.95 nincs pontosan benne a táblázatban, 0.9505-öt fogunk használni.
Az ehhez tartozó x érték 1.65 standard normális eloszlás esetén 1.65, amelyet most vissza kell számolnunk az N(28,4) eloszlás szerint. X=m +xs =28+1.65(4)=34.6 mm. Tehát, a 35 mm-nél hosszabb fogú denevérek esnek a populáció felső 5 % -ába, akiknek tehát halálos a harapása.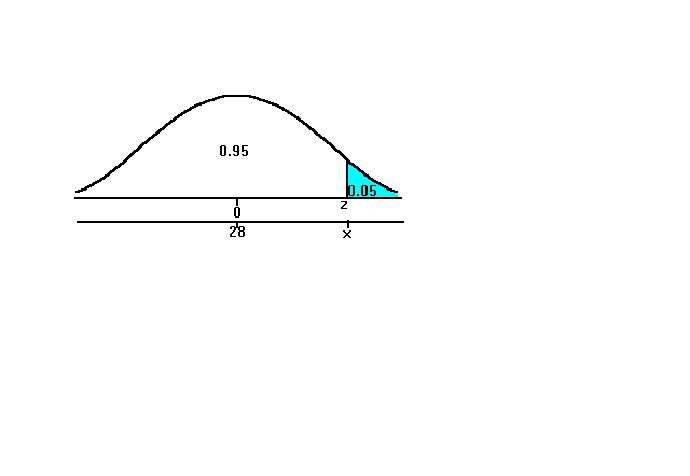
14. ábra.
Feladatok
1. Standard normális eloszlás esetén keressük meg azt az x értéket, amely a felső
a) 5 %-ot b)2.5 %-ot c)1 %-ot d)0.5 %-ot
vágja le az eloszlásból
2. Egy bizonyos vérvizsgálati teszt eredményéről ismert, hogy normális eloszlású N(60,18).
a) Az adatok hány százaléka esik 40 és 80 közé?
b) Hány százalék esik 60 alá?
c) Hány százalék esik az "egészséges tartományba", azaz 30 és 90 közé?
3. Egy városi kórházban az újszülöttek testsúlyai normális eloszlásúak N(3500,400) paraméterekkel. Legyen X egy véletlenszerűen kiválasztott újszülött súlya. Határozzuk meg a következő valószínűségeket:
a) P(X>4000)
b) P(3000<X<4000)
A mintaátlagok elméleti eloszlása.
Tekintsünk először egy példát. Egy fiatal ember, miután állást kínáltak neki egy nagy cégnél, megkérdezte a személyzeti titkárt, hogy mennyi az alkalmazott ügyintézők átlagéletkora. Az illető nem tudta a pontos választ, mivel több száz ügyintéző volt a vállalatnál, de körülnézett az irodában, és az ott lévő 38 ügyintéző életkora alapján 20-ra b
ecsülte az átlagéletkort. A fiatalember tulajdonképpen egyfajta hipotézisvizsgálatot végzett, amely a statisztikusok körében gyakori. A populáció m átlagára vonatkozó következtetésre jutott egy minta alapján.Képzeljük el, hogy ez a fiatal ember irodáról irodára jár, és mindegyikben kiszámítja az átlagéletkort. A nap végére átlagokból álló hosszú listája lesz. Egy ilyen lista a mintaátlagokból keletkezett minta.
Centrális határeloszlás tétel
A centrális határeloszlás tétel azt mondja ki, hogy nagy minta-elemszám esetén (mondjuk, n nagyobb, mint 30), az összes lehetséges mintaátlagokból álló populáció közelítően normális eloszlású lesz m
átlaggal és ![]() standard deviációval, azaz,
standard deviációval, azaz,
N(m
,![]() ) eloszlású lesz, függetlenül az eredeti populáció eloszlásától.( 15. ábra.)
) eloszlású lesz, függetlenül az eredeti populáció eloszlásától.( 15. ábra.)
Más szóval, egy populációból vett nagy elemszámú minták átlagai olyan populációból származnak, melynek eloszlása (az átlagolással nyert új populáció eloszlása):
1. Közelítőleg normális eloszlású
2. Az átlaga (az összes lehetséges minták átlagainak az átlaga) ugyanaz, mint a populáció átlaga , m .
3. A standard deviáció kisebb az eredeti populáció standard deviációjánál: =![]() .
.
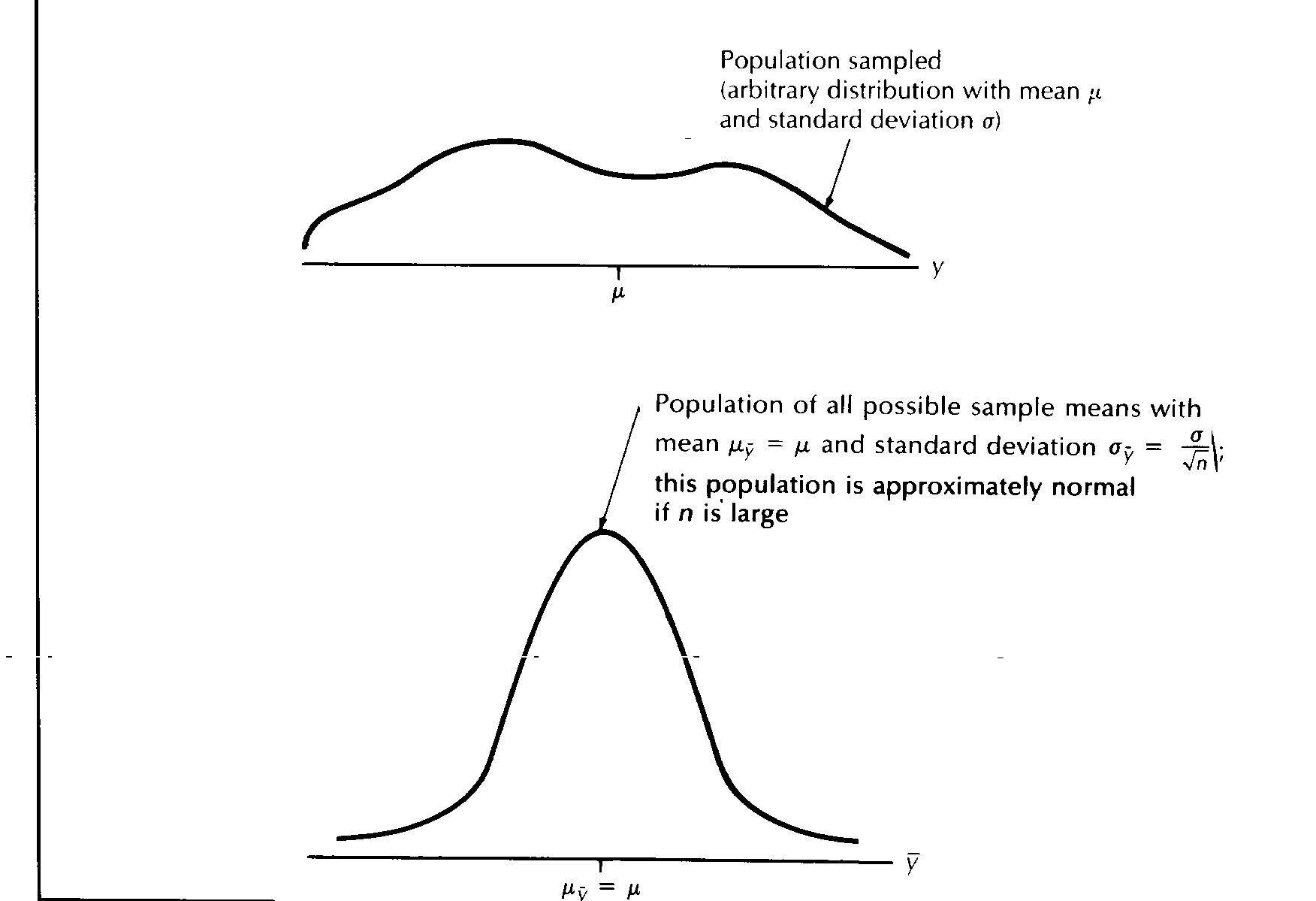
15. ábra.
Ha egy populáció bármely elemének értékét rengeteg apró véletlenszerû hatás összegezõdése határozza meg (pl. a testsúlyt a táplálkozás sok összetevõje, testmozgás, genetikai tényezõk, stb.), akkor a centrális határeloszlás tétel alapján a populáció eloszlása közelítõleg normális. A centrális határeloszlás tétel egy gyakorlati alkalmazása az, amikor "segítünk a természetnek": ha egy mérésnél a hiba eloszlása nem eléggé normális, akkor a mérés kellõ számú ismétlésébõl számolt átlag már jobban közelíti a normális eloszlást, kisebb szórással.