IV. Statisztikai becslés, konfidencia intervallumok.
4.1. Statisztika, konfidencia intervallum
Az adatelemzés egy tipikus problémája a következõ. Ismert a populáció eloszlásának általános matematikai formulája, de egy vagy több paraméter értéke nem, ezeket egy mintából kell becsülni. Például, ismert, hogy a testsúlyok normális eloszlást követnek, de a populáció paraméterei, m és s ismeretlenek, ezeket kell egy minta alapján közelítõleg meghatároznunk. Ez a paraméterbecslés problémája.
Definíció.
Az ![]() mintaelemek függvényét (amely maga is valószínûségi változó) statisztikának nevezzük. n
mintaelemek függvényét (amely maga is valószínûségi változó) statisztikának nevezzük. n
Jól ismert példa: az ![]() statisztika (a minta átlag) becslése a populáció átlagnak, m
-nek. Hasonlóan, az s statisztika, a minta standard deviáció a populáció standard deviációjának, s
-nak a becslése, és s
statisztika (a minta átlag) becslése a populáció átlagnak, m
-nek. Hasonlóan, az s statisztika, a minta standard deviáció a populáció standard deviációjának, s
-nak a becslése, és s
Konfidencia intervallumok.
A legtöbb statisztikai alkalmazásban nem elegendõ azt állítani, hogy a paraméter többé kevésbé megközelíthetõ statisztikákkal. Sokszor van szükség olyan intervallum megadására, amely a populációbeli paraméter értékét nagy valószínûséggel tartalmazza. Értékeknek egy ilyen halmazát intervallumbecslésnek nevezzük. Egy ilyen intervallum mindig kapcsolatba hozható egy valószínûséggel . Minél nagyobb valószínûséget rendelünk az intervallumhoz, annál biztosabbak lehetünk abban, hogy az intervallum tartalmazza a paraméter igazi értékét.
Definíció
Legyen a egy populáció paramétere, a
egy tetszõlegesen választott (kis) valószínûség, ![]() egy minta. Ha tudunk olyan a
egy minta. Ha tudunk olyan a
![]() ,
,
akkor az (a
1, a2) véletlen intervallumot az a paraméterre vonatkozó konfidencia intervallumnak nevezzük, az (1-a )100% számot konfidencia vagy megbízhatósági szintnek . na -t általában a =0.1, a =0.05, a =0.01 vagy a =0.001-nek szokás választani, és így a megfelelõ megbízhatósági szintek 90%, 95%, 99% vagy 99.9%.
4.2. Konfidencia intervallum normális eloszlású populáció m paraméterére ismert standard deviáció esetén.
Ha ![]() N(m
,s
) eloszlású populációból vett minta, akkor a
N(m
,s
) eloszlású populációból vett minta, akkor a
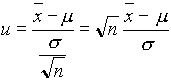 (4.1)
(4.1)
valószínûségi változó N(0,1) eloszlású. Ha a >0 adott, meg lehet adni az eloszlás felsõ és alsó a /2 százalékát levágó pontokat. Jelölje ezeket ua
/2 és -ua /2. Így![]() (4.2)
(4.2)
A (4.1)-ben megadott u-t (4.2)-be helyettesítve, majd m -t kifejezve kapjuk, hogy
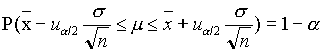 (4.3)
(4.3)
azaz, az 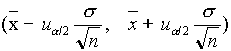 véletlen intervallum a m
-t tartalmazza 1-a
valószínûséggel. Ez tehát egy (1-a
)100% szintû konfidencia intervallum m
-re .
véletlen intervallum a m
-t tartalmazza 1-a
valószínûséggel. Ez tehát egy (1-a
)100% szintû konfidencia intervallum m
-re .
Adott a esetén ua
/2 a normális eloszlás táblázataiban megtalálható. Ha a =0.05, a /2=0.025, F (1.96)=0.975, tehát ua /2 =1.96. Hasonlóan, ha a =0.01, ua /2 =2.58.4.3. Konfidencia intervallum normális eloszlású populáció m paraméterére ismeretlen standard deviáció esetén.
Ha nemcsak m , de s is ismeretlen, akkor az õ becslését, a minta standard deviációját, s-t kell használnunk. Az u helyett egy másik, t-vel jelölt statisztikát fogunk alkalmazni, amely u -tól csak a nevezõben tér el:
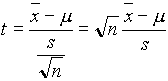 (4.4)
(4.4)
Ha az ![]() minta N(m
,s
) eloszlásból származik, akkor a t valószínûségi változó ún. t eloszlást vagy Student t eloszlást követ n-1 szabadságfokkal.
minta N(m
,s
) eloszlásból származik, akkor a t valószínûségi változó ún. t eloszlást vagy Student t eloszlást követ n-1 szabadságfokkal.
A t- eloszlás
W.S. Gossett angol statisztikus volt, aki egy sörgyárban dolgozott, ahol kis elemszámú mintákat vizsgált. 1908-ban írt egy cikket "A. Student" álnéven, amelyben a kis minták tulajdonságait vizsgálta. Alapvetõen, kis minták esetén az s értéke nagyon ingadozó lehet, tehát, ha valamelyik kísérletben az s-et használjuk a ![]() formulában, a kapott konfidencia intervallum szintje valójában kisebb lesz, mint azt ua
/2 alapján gondolnánk. Hogy ezt a problémát megoldjuk, a normális eloszlás helyett a Student-féle t eloszlást kell használnunk.
formulában, a kapott konfidencia intervallum szintje valójában kisebb lesz, mint azt ua
/2 alapján gondolnánk. Hogy ezt a problémát megoldjuk, a normális eloszlás helyett a Student-féle t eloszlást kell használnunk.
Sok t eloszlás van, minden szabadságfokhoz ( a minta-elemszámtól függõ számhoz) különbözõ t-eloszlás tartozik. A t-eloszlások hasonlóak a normális eloszláshoz, szimmetrikusak és harang alakúak. Ha pontosan lerajzoljuk, látható, hogy minél kisebb a szabadságfok, annál laposabb a görbe. Fordítva, minél nagyobb a szabadságfok, annál jobban "hasonlít" a t-eloszlás görbéje a normális eloszlás görbéjére. A t-eloszlásokat a különbözõ szabadságfokok szerinti táblázatokban megtalálhatjuk.
Ha a >0 adott, megadhatjuk az n-1 szabadságfokú t-eloszlás azon pontjait, melyek a felsõ és alsó a /2 százalékot vágják le. Jelölje ezeket ta
/2 és -ta /2. A következõ egyenlõség érvényes:![]() (4.5)
(4.5)
Behelyettesítve (4.4)-beli t-t (4.5)-be, és m -t kifejezve kapjuk, hogy
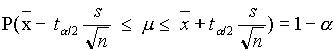 (4.6)
(4.6)
azaz, a 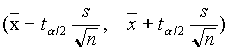 véletlen intervallum tartalmazza m
igazi értékét. Ez az intervallum tehát (1-a
)100% szintû konfidencia intervallum m
-re.
véletlen intervallum tartalmazza m
igazi értékét. Ez az intervallum tehát (1-a
)100% szintû konfidencia intervallum m
-re.
Szabadságfok
Hogy a t táblázatot használhassuk, meg kell találnunk azt a "sort", amely az adott elemszámnak megfelel. Tehát egy olyan táblázatot képzelhetnénk el, amelynél egy n-nel jelzett elsõ oszlop tartalmazza a minta elemszámát. Csakhogy elõfordul, hogy ugyanezt a táblázatot más problémáknál is használnunk kell (például, két különbözõ elemszámú minta esetén), ahol ennek az elsõ oszlopnak nem lenne értelme. Ezért inkább a szabadságfok elnevezést használják ennek az elsõ oszlopnak a jelölésére. Nem nyilvánvaló, hogy miért. Technikai szempontból azért, mert ugyanez a t-eloszlás egy másik, késõbb tanulmányozandó eloszlással (az ún. c
2 eloszlással) van kapcsolatban, amely eloszlásnál a szabadságfok elnevezésnek szemléletesebb jelentése van. Nekünk elegendõ azt tudni, hogy a populáció átlagára vonatkozó hipotézisnek a tesztelésénél, amelynél egyetlen mintával dolgozunk, a szabadságfok értéke n-1.4. Példa. Egy cég 16 ml-es üvegekben árul bizonyos gyógyszert. Az üvegeket egy automata tölti. Ha nem tölt pontosan, tehát többet vagy kevesebbet tölt az üvegekbe, akkor a töltést le kell állítani és újra beállítani az automatát. A cég csak akkor állítja le a folyamatot, ha nagyon biztos abban, hogy az átlagos töltés a 16 ml alatt vagy felett van.
Az automata adott beállítása esetén az összes lehetséges legyártott vagy legyártható üvegek (végtelen) populációjáról van szó, amely populáció átlaga, m =16. A gyártás ellenõrzésére idõnként véletlenszerûen kiválasztanak néhány üveget (minta), ennek alapján próbálnak következtetni a populációra.
Tegyük fel, hogy a következõ, hatelemû mintát kapták az egyik ellenõrzés során:
15.68, 16.00, 15.61, 15.93, 15.86, 15.72
Számítsunk 95%-os és 99%-os konfidencia intervallumot a minta alapján a populáció átlagára.! Könnyen ellenõrizhetõ, hogy az átlag ![]() és a szórás s=0.156
és a szórás s=0.156![]() .
.
95%-os konfidencia intervallum számításához a fentieken kívül még az a =0.05 valószínûséghez és n-1=5 szabadságfokhoz tartozó táblázatbeli t-értékre van szükségünk. Ez ta
/2 =2.57. Így a 95%-os konfidencia intervallum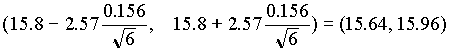 .
.
Annak valószínûsége, hogy az automata adott állapotának megfelelõ populáció átlaga ebbe az intervallumba esik, 0.95 (95%). Ha másik 100, hatelemû mintát vennénk a fenti állapot mellett, akkor ezek átlagai közül 5 nem fog beleesni a fenti intervallumba.
99%-os konfidencia intervallum számításához a fentieken kívül még az a =0.01 valószínûséghez és n-1=5 szabadságfokhoz tartozó táblázatbeli t-értékre van szükségünk. Ez ta
/2 =4.032. Így a 99%-os konfidencia intervallum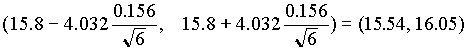 . Látható, hogy az intervallum szélesebb lett. Ha nagyobb biztonsággal szeretnénk megállapítani a paraméter valódi értékét, az intervallum hossza nagyobb lesz.
. Látható, hogy az intervallum szélesebb lett. Ha nagyobb biztonsággal szeretnénk megállapítani a paraméter valódi értékét, az intervallum hossza nagyobb lesz.
Az átlag szórása (standard error of mean).
Látható, hogy a populáció paraméterének értéke egy olyan intervallumba esik, amely szimmetrikus az ![]() mintaátlagra. Nagy elemszám esetén (n>30) és a
=0.05 esetén, a ta
értéke körülbelül 2. Így a 95 % -os konfidencia intervallum hossza az
mintaátlagra. Nagy elemszám esetén (n>30) és a
=0.05 esetén, a ta
értéke körülbelül 2. Így a 95 % -os konfidencia intervallum hossza az ![]() mennyiségtõl függ. Ennek a számnak speciális jelentése van, mivel a centrális határeloszlás tételben említett
mennyiségtõl függ. Ennek a számnak speciális jelentése van, mivel a centrális határeloszlás tételben említett ![]() becslésének tekinthetõ.
becslésének tekinthetõ.
Definíció
A 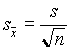 képlettel megadott statisztikát az átlag szórásának nevezzük, vagy standard errornak (rövidítése néha S.E.M.). n
képlettel megadott statisztikát az átlag szórásának nevezzük, vagy standard errornak (rövidítése néha S.E.M.). n
Ez a szóródásnak egy másik mérõszáma. Különbséget kell, hogy tegyünk a két tanult szórás között: a standard deviáció a mintaelemek szóródását fejezi ki az átlag körül, míg a standard error az összes lehetséges mintaátlag szóródását fejezi ki a populáció átlaga körül. Ha megismétlünk egy kísérletet, akkor az új átlag a régitõl a (4.3)-beli formulának megfelelõ intervallumban fog feküdni 1-a valószínûséggel.
A minta elemszámának meghatározása
Tegyük fel, hogy szeretnénk meghatározni a minta n elemszámát oly módon, hogy (1-a )100% biztonsággal elõírjuk, hogy a mintaátlag d egységgel térhet el maximálisan a populáció átlagától. Ha (4.3)-ban a határokat egyenlõvé tesszük d-vel és ezt az egyenletet megoldjuk n-re, a következõt kapjuk .
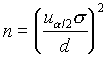 . (4.4)
. (4.4)
Ez a formula tartalmazza a populáció standard deviációt, s -t, amely sokszor nem ismert, egy mintából kell becsülnünk. Ha egy hasonló, megelõzõ vizsgálat során n
p elembõl kiszámoltuk a standard deviációt, és ha np-1 legalább 30 volt, akkor n-et a (4.4). szerint számolhatjuk. Ha np-1 kevesebb volt, mint 30, akkor n-et a következõ formula szerint számolhatjuk: