és a szórás s=0.156
.V. Hipotézisvizsgálatok (statisztikai próbák)
Gyakran a vizsgálatok, kísérletek adatainak kiértékelése nem csak arra irányul, hogy az adatokat összesítsük. hanem arra is, hogy az adatok alapján következtetéseket vonjunk le a populáció(k)ra vonatkozóan. A statisztikai próbákkal bizonyos, a populáció(k)ra vonatkozó feltevéseket (hipotéziseket) ellenõrzünk.
Példa. Egy cég 16 ml-es üvegekben árul bizonyos gyógyszert. Az üvegeket egy automata tölti. Ha nem tölt pontosan, tehát többet vagy kevesebbet tölt az üvegekbe, akkor a töltést le kell állítani és újra beállítani az automatát. A cég csak akkor állítja le a folyamatot, ha nagyon biztos abban, hogy az átlagos töltés a 16 ml alatt vagy felett van.
Az automata adott beállítása esetén az összes lehetséges legyártott vagy legyártható üvegek (végtelen) populációjáról van szó, amely populáció átlaga, m =16. A gyártás ellenõrzésére idõnként véletlenszerûen kiválasztanak néhány üveget (minta), ennek alapján próbálnak következtetni a populációra.
Tegyük fel, hogy a következõ, hatelemû mintát kapták az egyik ellenõrzés során:
15.68, 16.00, 15.61, 15.93, 15.86, 15.72
Könnyen ellenõrizhetõ, hogy az átlag és a szórás s=0.156.
A példa során felmerülõ kérdések:
Igaz-e az, hogy az automata pontosan mûködik?
Mit jelent pontosabban az, hogy nagyon biztos?
Mekkora hibát követünk el, ha azt állítjuk, hogy jól tölt az automata, de valójában rosszul tölt?
Mekkora hibát követünk el, ha azt állítjuk, hogy rosszul tölt az automata, de valójában nem ez a helyzet?
Statisztikai hipotézisek
Tekintsük a következõ kérdéseket.
1. A tüdõrákos betegek hány százaléka dohányzott?
2. Mennyivel hatásosabb az A gyógyszer, mint B?
3. Igaz-e, hogy a vásárlók 30 %-a a kedvenc fogkrémjét vásárolja, függetlenül az ártól?
4. Igaz-e, hogy egy gyógyszertöltõ automata átlagosan 16 ml-re tölti fel az üvegeket?
5. Más-e a fiúk és lányok matematika vizsgaeredménye?
Ezek a kérdések két csoportba sorolhatók. Az 1. és 2. kérdésre egy szám a válasz. Az utolsó háromra igen-nem válasz adható, tehát eldöntendõ kérdések. A statisztikusok gyakran úgy használják ezeket a típusú kérdéseket, hogy elõzõleg kialakítanak két ellentétes állítást, az úgynevezett hipotéziseket. A statisztikai hipotézis egy populációra, vagy annak valamely paraméterére vonatkozó állítás. A 3., 4., 5. kérdések alapján a következõ hipotézis-párokat lehet felállítani:
3. Legyen p=P(a vásárlók a kedvenc fogkrémjüket vásárolják, függetlenül az ártól). Ekkor a két hipotézis:
H0: p=0.3 (a vásárlók 30 % -a vásárolja a kedvenc fogkrémet az ártól függetlenül.)
H1: p¹ 0.3 (az a százalék, amely a kedvenc fogkrémjét vásárolja, különbözik 30 %-tól.)
4. H0: m =16 (a populáció átlaga 16)
H1: m ¹ 16 (a populáció átlaga nem 16)
5. H0: m
H1: m
F¹ m L (a fiúk ás lányok populáció-átlaga nem ugyanaz)Nullhipotézis, alternatív hipotézis
A statisztikusok általában azt a hipotézist tesztelik, amely azt mondja meg, mi várható abban az esetben, ha a populáció paramétere egy specifikus értéket vesz fel, tehát ha a populáció paramétere egyenlõ egy adott számmal. Ezt a hipotézist nullhipotézisnek szokták nevezni, a jelölése H
0. A nulhipotézisben általában az egyenlõséget, a hibátlanságot tételezzük fel. Az ezzel szembenálló hipotézis, amely a különbözõséget tételezi fel, alternatív hipotézisnek nevezzük, jelölése Ha. Általában ez a bennünket érdeklõ hipotézis, ha éppen a változást (a kezelés, gyógyszer hatásosságát) szeretnénk bebizonyítani. Némely statisztikus Ha-t motivációs hipotézisnek nevezi.Térjünk vissza a 3., 4. és 5. kérdésekre. Vajon melyik a nullhipotézis, és melyik az alternatív a felsorolt hipotézis-párok közül ?
A 3. kérdésre, ha 200 vásárlót megkérdeznénk, hánytól várható "igen" válasz? Ha H0 igaz, várhatóan 60 vásárló fog igennel válaszolni (200-nak a 30 %-a 60). Ha H1 igaz, nem tudjuk bizonyosan, mi várható, csak annyi, hogy nem 60 . Tehát H0 a nullhipotézis, H1 az alternatív.
A 4. kérdés esetén, ha H0 igaz, azt várjuk, hogy a populáció-átlag 16, tehát ez a nullhipotézis.
Az 5. kérdés esetén tegyük fel, hogy 50 fiút és 50 lányt tesztelünk, és kiszámítjuk az átlagokat mindkét csoportban. Ha H0 igaz, azt várjuk, hogy a két átlag megegyezik, a kapott különbséget a véletlen okozza.
A fenti kérdések mindegyikében a H0 a nullhipotézis. A 4. példa esetén a nullhipotézis az, hogy a populáció várható értéke 16, az alternatív hipotézis az, hopgy a populáció várható értéke különbözik 16-tól.
Összefoglalva, a nullhipotézis a populáció paraméterének egy speciális értékére vonatkozó állítást jelent. Ez az egyenlõségjel (=) használatában nyilvánul meg. Az alternatív hipotézist a nem egyenlõ (¹ ), vagy a kisebb, nagyobb jelek megjelenése jellemzi (< ,> ).
Döntési szabályok
A kísérlet kezdetén két hipotézist állítunk fel, a hipotézisvizsgálat során döntenünk kell valamelyik mellett. Ez a döntés valamilyen szabály szerint történik. A döntési szabályok függnek az adatok típusától, a kérdésfeltevéstõl (a null- és alternatív hipotézistõl), és még egyéb feltételektõl, pl. attól, hogy mekkora hibát engedjünk meg magunknak, ha az alternatív hipotézis mellett döntünk. Ennek a hibának a valószínûségét a -val jelölik és általában a =0.05 érték mellett rögzítik. A döntés eredményeként dönthetünk az alternatív hipotézis mellett, ekkor azt mondjuk, hogy "elvetjük a nullhipotézist", a különbség szignifikáns (1-a )100%-os szinten. .Ha a a nullhipotézis mellett döntünk, akkor azt mondjuk, hogy "nem tudjuk elvetni a nullhipotézist", a különbség nem szignifikáns (1-a )100%-os szinten.
Statisztikai hibák.
Hipotézisvizsgálat során tehát a minták alapján az összehasonlítandó populációkról döntést hozunk: vagy azt állítjuk róluk, hogy különbözõk, vagy azt, hogy azonosak.
Bárhogyan döntünk is, nem tudhatjuk, hogy helyesen döntöttünk-e, mivel a valóságot nem ismerjük (a hipotézisvizsgálatot éppen ezért végezzük). Helyesen döntöttünk, ha különbséget állapítottunk meg és a populációk valóban eltérõk, vagy ha nem állapítottunk meg különbséget, és a populációk valóban azonosak.
Elõfordulhat, hogy szignifikáns különbséget állapítunk meg, pedig valójában nincs különbség. Ebben az esetben a döntés hibás, az elkövetett hibát elsõ fajta hibának nevezik, nagyságát elkövetésének valószínûségével szokás megadni. Az elsõ fajta hiba valószínûsége annak esélye, hogy a tapasztalt különbséget a véletlen okozta, ez éppen a szignifikancia-szinttel egyenlõ (a ).
Az is elõfordulhat, hogy a minták alapján nem állapítunk meg szignifikáns különbséget, pedig valójában, azaz a populációk között mégis van különbség. Ebben az esetben a döntés hibás, az így elkövetett hibát második fajta hibának nevezik.
A második fajta hiba valószínûségét (b ) általában nem ismerjük, mivel függ pl. a szignifikancia szinttõl, az elemszámtól, a populáció(k) szórásától és a tényleges különbség (hatás) nagyságától. A ~ valószínûségének kiszámítását az nehezíti, hogy nem ismerjük a populációk közötti tényleges különbséget, így gyakran ehelyett a megfelelõnek tekintett (legkisebb jelentõs különbséget), vagy a minták átlagai alapján becsült különbséget alkalmazzák. A populáció szórását pedig a minta(ák)ból számolt szórással közelítik.
Pl. 5%-os szignifikancia szint esetén, amennyiben a populációk között nincs különbség, az elsõ fajta hiba elkövetésének valószínûsége 0.05, azaz minden száz ilyen esetbõl 5 alkalommal, nagyjából minden húszadik esetben követjük el ezt a hibát. Ennyiszer okoz ugyanis a véletlen a különben egyforma, azonos populációkból vett minták közt túlságosan nagy, általunk szignifikánsnak minõsített különbséget.
A 4. táblázatban foglaljuk össze a lehetséges eseteket.
|
nem vetjük el H 0-t |
elvetjük H 0-t |
|
|
H 0 igaz |
helyes |
elsõ fajta hiba |
|
H 0 hamis |
második fajta hiba |
helyes |
A hibák valószínûségeinek jelölésére görög betûket használunk, az elsõ fajta hiba valószínûségét a -val, a második fajta hiba valószínûségét b -val jelöljük.
Nyilván azt szeretnénk, hogy mindkét fajta hiba valószínûsége kicsi legyen. Általában a hipotéziseket rögzített minta-elemszámra és rögzített a esetén tesztelik, szokásos értékei a =0.05 vagy a =0.01. Általában, rögzített minta-elemszám esetén minél kisebb az elsõ fajta hiba, annál nagyobb a második fajta hiba valószínûsége. Rögzített a esetén b a minta-elemszám növelésével csökken.
A próba ereje
b értékét nem tudjuk addig meghatározni, ameddig az alternatív hipotézis egy specifikus értékét nem rögzítettük. A statisztikában az 1 - b értéket a próba erejének nevezik. A próba ereje azt méri, hogy a próba milyen jó abban az esetben, ha elvetjük a hamis nullhipotézist. Minél erõsebb a próba, (minél közelebb van 1 - b értéke 1-hez), annál nagyobb valószínûséggel veti el a hamis nullhipotézist. Másképpen: a próba ereje annak valószínûsége, hogy egy különbséget — adott mintanagyság és szignifikancia-szint mellett — egy statisztikai próba kimutat. A vizsgálatok tervezésének gyakorlatában az erõ nagyságának elõre megszabott értékébõl kiindulva határozzák meg a szükséges mintaelemszámot.
A statisztika elméletének fontos része olyan döntési szabályok keresése, amely a próbát a lehetõ legerõsebbé teszi adott a esetén.
Egy- és kétoldalú próbák
Ha bebizonyosodik, hogy egy nullhipotézis hamis, három különbözõ alternatív hipotézist lehet konstruálni. Tegyük fel, hogy továbbra is a gyógyszertöltõ automata töltéseibõl vett 6 elemû mintát vizsgáljuk.
A nullhipotézis az, hogy a populáció átlaga m =16.
H
0: m =16.Az alternatív hipotézis a következõ három állítás valamelyike lehet:
1. A töltések átlaga kevesebb, mint 16, azaz H
a: m <16, az automata alultölt.2. A töltések átlaga több, mint 16, azaz H
a: m >16.3. Ha nincs okunk feltételezni, hogy több-e vagy kevesebb a populáció átlag 16-nál, akkor az alternatív hipotézis H
a: m
16.
Az elsõ két alternatív hipotézis esetén egyoldalú próbáról beszélünk, mivel a bennünket érdeklõ értékek a 16-tól egy irányban térnek el. A harmadik esetben kétoldalú próbáról beszélünk, mivel a 16-tól mindkét irányban eltérhetnek az alternatív hipotézisben szereplõ értékek.
Megjegyezzük, hogy a nullhipotézis felírásakor mindig egyenlõségjelet használjuk (=) , míg az alternatív hipotézisben egyoldalú próba esetén a kisebb (<) vagy a nagyobb (>) jel jelenik meg, kétodalú próba esetén a nemegyenlõ jel ().
A döntési szabály megalkotására példa normális eloszlású, ismeretlen szórású populáció átlagának a tesztelése esetén.
H0: m =c, Ha: m ¹ c.
a) Döntés konfidencia intervallum alapján
A 4. példában adott a esetén megalkottunk egy konfidencia intervallumot a populáció átlagára. Az intervallum tehát nagy valószínûséggel tartalmazza az átlag valódi értékét. Így ez az intervallum használható annak a hipotézisnek a tesztelésére, hogy a populáció átlaga egyenlõ-e egy adott számmal.
Ha az intervallum nem tartalmazza az adott számot, akkor a döntésünk az, hogy a populáció átlaga különbözik az adott számtól (1-a )100 % -os szinten, és azt mondjuk, hogy a különbség szignifikáns (1-a )100 %-os szinten.
Ha a konfidencia intervallum tartalmazza az adott számot, akkor döntésünk az, hogy a populáció átlaga azonos az adott számmal, a különbség nem szignifikáns
(1-a
)100 %-os szinten.
A 4. példában a H0: m =16 (a populáció átlaga 16) nullhipotézis és a H1: m ¹ 16 (a populáció átlaga nem 16) alternatív hipotézis között kellett döntenünk.
A 95 %-os konfidencia intervallum (15.64, 15.96) volt. Ez az intervallum nem tartalmazza a 16-ot, ezért 95%-os szinten szignifikáns a különbség, a döntésünk az, hogy a populáció átlaga nem 16, az automata tehát rosszul mûködik. E döntés esetén elkövetett hibánk valószínûsége 5% -nál kisebb (p<0.05).
A 99 %-os konfidencia intervallum (15.54, 16.05) volt. Ez az intervallum már tartalmazza a 16-ot, ezért 99%-os szinten nem szignifikáns a különbség, a döntésünk az, hogy a populáció átlaga 16. 1% hiba mellett tehát nem tudjuk azt mondani, hogy az automata rosszul tölt. (p>0.01).
Általában, amikor egy döntési szabályt megalkotunk, elõször le kell rögzítenünk. mekkora valószínûségû elsõ fajta hibát akarunk megengedni. Ha az elsõ fajta hiba valószínûsége a , az (1-a )100 % -ot a próba szignifikancia szintjének nevezzük. Ha a =0.05, a szignifikancia szint 95%.
b) Döntés kritikus érték alapján
Az elõbbi nullhipotézis tesztelésre más módon is kaphatunk döntési szabályt: a konfidencia intervallum helyett használhatjuk az ún. kritikus pontokat. Ha a nullhipotézis igaz, a (4.4)-beli statisztika n-1 szabadságfokú t-eloszlású :
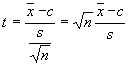(4.4)
Ha adott a >0, megadhatjuk a az n-1 szabadságfokú t-eloszlás azon pontjait, melyek a felsõ a /2 és alsó a /2 részét vágják le. Jelölje ezeket a pontokat ta
/2 és -ta /2. A következõ egyenlõséget kapjuk:
(4.5)
vagy
A döntési szabály a következõ: elvetjük H
0-t a valószínûségû elsõ fajta hibát követve el, ha
. Ellenkezõ esetben nem vetjük el H0-t, ekkor a második fajta hibát követjük el, amelynek valószínûségét nem is ismerjük.
A példában, a =0.05 esetén
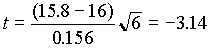, az n-1=5 szabadságfokhoz tartozó kritikus érték, ta
Itt |t|> ta
/2 , így a nullhipotézist elvetjük és azt mondjuk, hogy a különbség szignifikáns 95%-os szinten. 5% hibát feltételezve azt állítjuk, hogy a populáció átlaga nem 16. Másképpen: ha azt állítjuk, hogy a valódi átlag nem 16, akkor az elkövetett hibánk 5%-nál kisebb.a =0.01 esetén a kritikus érték ta
/2 =4.032, így |t|< ta /2, így a nullhipotézist 99%-os szinten nem tudjuk elvetni. 1% hibát megengedve nem tudjuk azt mondani, hogy a valódi átlag különbözik 16-tól. A különbség nem szignifikáns 99%-os szinten.c) Döntés p-érték alapján (számítógépes programok alkalmazása során)
A legtöbb számítógépes program tartalmazza a t próbát, de a t érték és a szabadságfok kiszámítása után általában nem a kritikus értéket számítja ki, hanem adott nullhipotézis és szabadságfok esetén a mintából számolt t értéktõl jobbra esõ, t-eloszlás alatti területet. Ezt a számot többféleképpen is nevezik: p-értéknek, Prob-value, Signif of t, Sig.Level, stb. Mi p-értéknek fogjuk nevezni. A p-érték tulajdonképpen annak valószínûsége, hogy egy másik kiszámolt t legalább olyan messze van 0-tól, mint a most megfigyelt t, ha H
0 igaz. A döntés a p-érték alapján úgy történik, hogy azt összehasonlítjuk a -val. Ha a p-érték kisebb, mint a , elvetjük a nullhipotézist és azt mondjuk, hogy a különbség szignifikáns (1- a )100%-os szinten, az ellenkezõ esetben nem vetjük el a nullhipotézist.Például az SPSS program One-Sample T-Test eljárása az alábbi eredményt adja:
A felsõ sorban a mintabeli jellemzõk találhatók, középen "Test Value" elnevezéssel a konstans értéke, amihez az átlagot hasonlítani szeretnénk, az alsó sorban az átlagok közötti különbség található, konfidencia intervallum a különbségre (az általunk kiszámított konfidencia. intervallum magára az átlagra vonatkozott, az itt található konfidencia. intervallum tehát 16-tal kisebb az általunk korábban kiszámítottnál.); az alsó sor jobboldali részén található a t-érték, df alatt a szabadságfok és 2-Tail Sig alatt pedig a p-érték. Látható, hogy a p-érték éppen 0.01 és 0.05 közé esik. Tehát a =0.05 esetén p<0.05, ezen a szinten a különbség szignifikáns, a =0.01 esetén p>0.01, ezen a szinten a különbség nem szignifikáns.
Number
Variable of Cases Mean SD SE of Mean
-------------------------------------------------------------
BOTTLE 6 15.8000 .153 .063
-------------------------------------------------------------
Test Value = 16
Mean 95% CI |
Difference Lower Upper | t-value df 2-Tail Sig
-------------------------------------------------------------
-.20 -.361 -.039 | -3.20 5 .024
-------------------------------------------------------------
A STATGRAPHICS nevû rendszer a következõ formában adja ugyanezt az eredményt:
Hypothesis Test for H0: Mean = 0 Computed t statistic = 3.32485
vs Alt: NE Sig. Level = 0.0126803
at Alpha = 0.05 so reject H0.
A Sig.Level =0.0126803, ez a p-érték, amely most kisebb, mint 0.05, tehát elvetjük H
0-t 95%-os szinten. Világos, hogy nem tudjuk elvetni H0-t 99%-os szinten, mivel 0.0126803>0.01.A hipotézisvizsgáló eljárások összefoglalása.
Azt az eljárást, amellyel a statisztikusok az adatokat elemzik annak eldöntésére, hogy van-e elegendõ bizonyíték a megsejtett (alternatív) hipotézis alátámasztására, hipotézisvizsgálatnak nevezzük. A következõ lépések foglalják össze a hipotézisvizsgálat általános menetét:
1. Az alternatív hipotézis megállapítása. Bizonyos elõzetes kísérletek vagy elgondolások alapján állítunk valamit, amelyet egy kísérlettel kívánunk bebizonyítani. Tehát, felállítjuk az alternatív hipotézist, H
a-t egy populációra vonatkozóan.2. A nullhipotézis megállapítása. Statisztikai meggondolások alapján az ellenkezõ hipotézist kell tesztelnünk. E célból megalkotjuk a nullhipotézist, H
0-t.3. a , azaz az elsõ fajta hiba, vagy az (1-a )100 % szignifikancia szint rögzítése. Azaz, megállapítjuk, mekkora hibavalószínûséggel akarjuk állítani, hogy az alternatív hipotézis igaz. Tetszõleges szignifikancia szinteket lehet választani. Mégis a legtöbb közleményben a =0.05 vagy a =0.01 szerepel. Ezek általánosan elfogadott standardok.
4. A véletlen minta elemszámának (n) meghatározása. Ezt a választást gyakran idõbeli és pénzbeli korlátok határozzák meg. A számítások egyszerûsítése is szempont lehet. Egyébként külön fejezete van a mintavételi módszereknek és az optimális minta-elemszám meghatározásának.
5. A véletlen minta kiválasztása a megfelelõ populációból, azaz a kísérlet elvégzése, melynek eredményeképpen megkapjuk az adatokat.
6. A döntési szabály kiszámítása. A döntési szabály egy vagy két kritikus pontot fog tartalmazni aszerint, hogy egy- vagy kétoldalú próbát végzünk-e.
7. Döntés az adatokból kiszámolt statisztika és az elõzõleg kiszámított döntési szabály alapján. A következõ döntések egyikét tesszük:
a) Elvetjük a nullhipotézist és azt állítjuk, hogy az alternatív hipotézis teljesül. Az elkövetett hibánk ilyenkor elsõ fajta hiba, valószínûsége a .
b) Nem vetjük el a nullhipotézist: nem tudtuk bebizonyítani, hogy az alternatív hipotézis igaz. Mivel nem határoztuk meg a próba erejét, és nem tudjuk a második fajta hiba nagyságát, nem állítjuk, hogy a nullhipotézis igaz. Ha a próba ereje alacsony, a második fajta hiba valószínûsége nagy. Így a "nem vetjük el a nullhipotézist" kifejezést használjuk inkább, mint az "elfogadjuk a nullhipotézist" kifejezést.
5.1. Hipotézisvizsgálat normális eloszlású populáció várható értékére: egymintás t-próba
Az elõzõekben bemutatott próba neve egymintás t-próba. Most általánosan is összefoglaljuk a próba lépéseit. Feltesszük, vagy korábbi ismereteink alapján tudjuk, hogy a vizsgált populáció normális eloszlású, de a paramétereit nem ismerjük. A próba a m paraméter értékére vonatkozik.
1. H0: m =c (c adott konstans).
2. Ha: m c (kétoldalú alternatív hipotézis)
3. a rögzítése
4. n meghatározása
5. Mintavétel, jelölje a keletkezett mintát 
.
6. A döntési szabály:
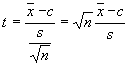és ta
/2 kiszámítása
7. Döntés:
esetén elvetjük a nullhipotézist és azt mondjuk, hogy a populáció átlagának c-tõl való eltérése szignifikáns (1-a
)100%-os szinten;
esetén nem vetjük el a nullhipotézist és azt mondjuk, hogy a populáció átlagának c-tõl való eltérése nem szignifikáns (1-a
)100%-os szinten.
5.2. Egymintás t-próba önkontrollos kísérletek kiértékelésére (összefüggõ minták esetén)
Az egymintás t-próbát a klinikai vizsgálatokban leggyakrabban nem egy, hanem két összefüggõ minta összehasonlítására használják, olyan esetben, amikor a kísérleti egyedeken a vizsgált változót kétszer egymás után megmérik. Az elsõ mérés általában a kezelés elõtti (kontroll) mérés, a második pedig általában a kezelés utáni érték. Az ilyen típusú kísérletet önkontrollos kísérletnek nevezzük.
Pl. tegyük fel, hogy egy kutató szeretné bebizonyítani, hogy egy bizonyos kezelés csökkenti a vérnyomást. Ehhez elõször megméri egy magas vérnyomásos populációból véletlenül választott csoport vérnyomását. Ezek az adatok adják a "kezelés elõtt" mintát. A kezelés után újból megméri ugyan azoknak az embereknek a vérnyomását, így keletkezik a "kezelés után" minta. A kezelés hatásosságát úgy lehet kimutatni, hogy kivonjuk a "kezelés utáni" és a "kezelés elõtti" adatokat minden egyes beteg esetén. Így egy harmadik mintát kapunk, amely a különbségekbõl áll. Összefoglalva általában a következõ adatokat kapjuk:
|
Kezelés elõtt |
Kezelés után |
Különbség |
|
x 1 |
y 1 |
d 1 |
|
x 2 |
y 2 |
d 2 |
|
. . |
. . |
. . |
|
x n |
y n |
d n |
Ha a kezelés hatásos volt, a különbség-minta átlagának 0-tól különböznie kell. Tehát a következõ nullhipotézist kell vizsgálnunk:
H
0: m =0 (a különbségek populáció-átlaga 0)H
a:
(a különbségek populáció-átlaga nem 0)-(kétoldalú próba), vagyH
(a különbségek populáció-átlaga kisebb vagy nagyobb, mint 0)-(egyoldalú próba).
Ez a szituáció speciális esete az egymintás t-próbának. Ha feltesszük, hogy a d-k populációja normális eloszlású, akkor a kísérletünk egymintás t-próbával kiértékelhetõ, ahol most a minta a d különbségek mintája, c pedig 0. A nullhipotézist tehát a következõ statisztikával tesztelhetjük:
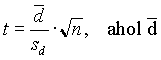a d különbségek átlaga, s
Adott a -hoz és n-1 szabadságfokhoz meghatározzuk (pl. táblázatból) ta
/2-t.A döntés: elvetjük H
0-t a valószínûségû elsõ fajta hibát elkövetve, ha
. és elfogadjuk H0-t, ha 
.
Példa. Tegyük fel, hogy 8 önként vállalkozó beteg kezelése során a következõ systolés vérnyomásértékeket kaptuk:
a =0.05, és 7 -es szabadságfokhoz tartozó kritikus érték a t-eloszlás táblázatából t
0.025,7=2.365 .|
Kezelés elõtt |
Kezelés után |
Különbség |
|
170 |
150 |
20 |
|
160 |
120 |
40 |
|
150 |
150 |
0 |
|
150 |
160 |
-10 |
|
180 |
150 |
30 |
|
170 |
150 |
20 |
|
160 |
120 |
40 |
|
160 |
130 |
30 |
|
s d=18.077t =3.324 |
Döntés: t=3.324>2.365, tehát elvetjük H
0-t és azt mondjuk, hogy a populáció átlagok közötti különbség szignifikáns 95 %-os szinten. (A kezelés hatásos volt). A döntés hibája elsõ fajta hiba, valószínûsége 0.05. Ez azt jelenti, hogy ha ugyanilyen körülmények között megismételnénk a kísérletet, 0.05 valószínûséggel kapnánk nem szignifikáns eredményt.Nézzük meg, mi lenne, ha a -t 0.01-nek választottuk volna. Minden számítás ugyanaz, csak a kritikus érték más: t
0.005,7=3.499. Most t=3.324<3.499, tehát 99%-os szinten nem tudjuk elvetni a nullhipotézist, 1%-val dolgozva nincs elegendõ információnk a hatás kimutatására.Számítógépek használata . Az SPSS program Paired T-Test eljárása az alábbi táblázatot eredményezi. Itt a 2-tail Sig alatt található a p-érték (=0.013), amely szerint 95 %-os szinten szignifikáns a különbség.
t-tests for Paired Samples
Number of 2-tail
Variable pairs Corr Sig Mean SD SE of Mean
------------------------------------------------------------------
BEFORE 162.5000 10.351 3.660
8 .067 .875
AFTER 141.2500 15.526 .489
------------------------------------------------------------------
Paired Differences |
Mean SD SE of Mean | t-value df 2-tail Sig
----------------------------------|-------------------------------
21.2500 18.077 6.391 | 3.32 7 .013
95% CI (6.137, 36.363) |
5.3. Két független, normális eloszlású populáció átlagának összehasonlítása: kétmintás t-próba
Tegyük fel, hogy két független mintánk van, melyeknek az elemszáma sem szükségképpen egyenlõ: 
. A két populáció átlagának teszteléséhez fel kell tennünk a következõket:
1. Mindkét populáció közelítõen normális eloszlású.
2. A két populáció varianciái megegyeznek.
Tehát, az xi-k N(m 1, s ) és az yi-k N(m 2,s ) eloszlású populációból származnak.
A két hipotézis:
H0: m 1=m 2
H
a: m 1
m
2 (kétoldalú próba).
Rögzítsük a -t.
Ha a feltételek teljesülnek és a nullhipotézis igaz, a mintaátlagok különbsége a t-eloszlással hozható kapcsolatba. Jelölje 
a mintaátlagokat, és s
,
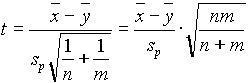statisztika n+m-2 szabadságfokú t-eloszlást követ . Itt
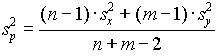
a közös variancia összevont (pooled) becslése.
A döntési szabályhoz meg kell keresnünk a táblázatból ta
/2, n+m-2 -t, ésa) ha | t| >ta
/2, n+m-2 , elvetjük a nullhipotézist,b) ha | t| <ta
/2, n+m-2 , nem vetjük el a nullhipotézist.Példa.
Tegyük fel, hogy a vérnyomást két különbözõ csoportban mértük meg, az egyik csoportot nem kezeltük (kontroll csoport, magas vérnyomásosok), a másodikat pedig kezeltük (kezelt csoport). Szeretnénk bebizonyítani, hogy a kezelés hatásos. A nullhipotézis az, hogy a két populáció átlaga megegyezik, az alternatív hipotézis szerint különbözõk. A kontroll csoportban 8, a kezelt csoportban 10 ember adatait vették fel, melyet a következõ táblázat tartalmaz:
A számított t érték = 6.6569 ,a kritikus t érték, t
0.025,16=2.12. Mivel 6.6569>2.12, elvetjük a nullhipotézist és azt állítjuk, hogy a két átlag közötti különbség szignifikáns 95% -os szinten. A kezelés tehát hatásos volt.|
Kontroll csoport |
Kezelt csoport |
|
170 |
120 |
|
160 |
130 |
|
150 |
120 |
|
150 |
130 |
|
180 |
110 |
|
170 |
130 |
|
160 |
140 |
|
160 |
150 |
|
130 |
|
|
120 |
|
|
n=8 |
n=10 |
Két normális eloszlású populáció szórásának összehasonlítása: F-próba
Tegyük fel, hogy két független mintánk van, melyeknek az elemszáma nem szükségképpen egyenlõ: 
. . A elõbbi t-próba végrehajtásának feltétele volt, hogy a szórások megegyeznek. Ezt fogjuk most tesztelni. Tegyük fel hogy az xi-k N(m
1, s
1) és az yi-k N(m
2,s
2) eloszlású populációból származnak.
A két hipotézis:
H0: s 1=s 2
H
a:s 1 > s 2 (egytoldalú próba).Rögzítsük a -t. Ha igaz a nullhipotézis,
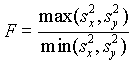
statisztika F-eloszlású . A F-eloszlás némiképp különbözik az eddigiektõl, nem szimmetrikus és két szabadságfoka van. Esetünkben az egyik szabadságfok a számlálóbeli minta elemszáma-1, a második a nevezõbeli minta elemszáma-1.
A táblázatok általában az egyoldali eset kritikus értékeit tartalmazzák. Miután megkerestük a kritikus F
tábla értéket, a döntésünk a következõ:F > F
tábla esetén elvetjük a nullhipotézist, a két variancia különbözikF < F
tábla esetén nem vetjük el a nullhipotézist, a két variancia nem különbözik (1-a )100%-os szinten.Példa.
Az elõzõ fejezet példájában feltettük, hogy a két variancia azonos, de nem ellenõriztük. Számítsuk ki az F értéket:
,
A számláló szabadságfoka 10-1=9, a nevezõé 8-1=7, a 9,7 szabadságfokokhoz tartozó kritikus F érték Fa
,9,7=3.68. Mivel 1.2029<3.68, a két szórás egyenlõségének a nullhipotézisét nem vetjük el.5.4. Két független, normális eloszlású populáció átlagának összehasonlítása különbözõ szórások esetén
Tegyük fel, hogy két független mintánk van, melyeknek az elemszáma nem szükségképpen egyenlõ: . Tegyük fel hogy az x
H
0: m 1=m 2H
a: m 1¹ m 2 (kétoldalú próba).Rögzítsük a -t. Ha igaz a nullhipotézis,
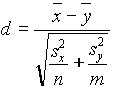statisztika t-eloszlást követ. A szabadságfok kiszámítása:
szab. fok=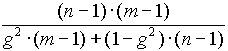
, ahol 
.
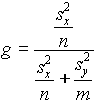Ez a szabadságfok nem lesz egész szám, ezért a táblázat használatakor kerekítenünk kell.
Az SPSS program alkalmazása kétmintás t-próba végrehajtására:
a) Adatbeírás: az adatokat úgy kell elrendezni, hogy egy változó tartalmazza a mért értékeket (Test Variable), és egy másik változó tartalmazza a csoportok kódjait (Grouping Variable). Esetünkben a következõ két változót kellett létrehoznunk:
GROUP BLOOD
1.00 170.00
1.00 160.00
1.00 150.00
1.00 150.00
1.00 180.00
1.00 170.00
1.00 160.00
1.00 160.00
2.00 120.00
2.00 130.00
2.00 120.00
2.00 130.00
2.00 110.00
2.00 130.00
2.00 140.00
2.00 150.00
2.00 130.00
2.00 120.00
A próba elvégzése SPSS-ben:
válasszuk a Statistics menüben a Compare Means almenüt, itt pedig az Independent-Samples T-test . A megjelenõ ablakba beírjuk:Test Variables: ide kell bevinni az összehasonlítandó változó nevét (blood)
Grouping Variable: csoportosító változó, amelynek az értékei szerint csoportokat képezünk (group)
Define Groups: A két kérdõjel azt jelzi, hogy be kell írnunk a csoportosító változó azon értékeit, amelyek szerinti csoportokat össze szeretnénk hasonlítani. Mivel az adatfile-ban a "group" változóban 1 és 2 szerepel, ezt a két értéket írjuk be az ablakokba.
Options: nem érdekes
Eredmények:
t-tests for Independent Samples of GROUP
Number
Variable of Cases Mean SD SE of Mean
------------------------------------------------------------------
BLOOD
Control 8 162.5000 10.351 3.660
Treatment 10 128.0000 11.353 3.590
------------------------------------------------------------------
Mean Difference = 34.5000
Levene's Test for Equality of Variances: F= .008 P= .930
t-test for Equality of Means 95%
Variances t-value df 2-Tail Sig SE of Diff CI for Diff
------------------------------------------------------------------
Equal 6.66 16 .000 5.183 (23.513, 45.487)
Unequal 6.73 15.67 .000 5.127 (23.613, 45.387)
------------------------------------------------------------------
A t-próba eredménye az alsó sorban van, a döntésünkhöz a "2-tail.Sig" alatt található p-érték szükséges. Ha ez a p kisebb, mint 0.05 (ill. az általunk rögzített a ), akkor a különbség szignifikáns 95%-os (ill. (1-a )100%-os szinten). Két sor is található ebben az alsó táblázatban, az elsõ (Equal) egyenlõ szórások, a második különbözõ szórások esetére.
Azt, hogy a szórások különböznek-e, vagy sem, nekünk kell eldöntenünk, mégpedig a két táblázat között található Levene's Test for Equality of Variances sor végén található p érték szerint. Esetünkben a szórások egyenlõségére vonatkozó teszt nem szignifikáns (p=0.93) , tehát a t-próba eredményét a felsõ sor "2-tail.Sig" alatt található p-értéke alapján dönthetjük el. Most ez a p=0.000, p<0.05, tehát szignifikáns a különbség 95%-os szinten. A p=0.000 nem jelenti azt, hogy a p -érték egyenlõ 0-val, csak azt, hogy nagyon kicsi, tehát kisebb, mint pl. 0.0001.
Feladatok
1. Számítsuk ki a standard errort, ha a minta elemszáma n=16 és a standard deviáció sd=5.6.
Ha a minta átlaga 12, mit tudunk mondani a mintaelemekrõl és az átlag megbízhatóságáról (a =0.05) ?
2. Számítsuk ki az átlagot, a mediánt és a szórást a következõ 4 elemû minta adatai alapján:
1 2 4 1
3. Egy vizsgálatban 10 egészséges nõ systolés vérnyomását mérve, az átlagra 119-et, a standard deviációra 2.1-et kaptak.
a) mennyi a standard error becslése?
b) számítsunk 95%-os konfidencia intervallumot a populáció átlagára.
c) milyen feltevés szükséges a kapott konfidencia intervallum érvényességéhez?
4. Egy vérnyomáscsökkentõ gyógyszer kipróbálásakor a következõ adatokat kapták
Gyógyszer nélkül Gyógyszer után
140 120
120 110
150 140
140 150
140 140
A különbség átlaga 6, a különbség standard deviációja 11.4.
Hatásos-e a gyógyszer (van-e különbség a két csoport átlagában)?
Végezzük el a számítást kézzel, a szignifikanciát állapítsuk meg táblázatból.
Ellenõrizzük az eredményt az SPSS -sel!
5. Egy lázcsillapító gyógyszer kipróbálásakor a következõ adatokat kapták
Gyógyszer után - Gyógyszer elõtt (különbségek)
1
0.5
1.5
-0.5
1
Hatásos-e a gyógyszer (eltér-e a különbség-átlag 0-tól)? (Átlag=0.7, sd=0.76)
Végezzük el a számítást kézzel, a szignifikanciát állapítsuk meg táblázatból.
Ellenõrizzük az eredményt az SPSS -sel!
6. Egy kutató egy új fájdalomcsillapító szer tesztelésénél a következõ eredményeket kapta.
Kontroll csoport (régi szer)elemszám=6, átlag=1.7 st.dev=0.8
Kezelt csoport (új szer) elemszám=7, átlag=2.3 st.dev=0.9
A t-próba eredménye p=0.234. A kutató azt álította mindezek alapján, hogy a két szer hasonló hatású.
a) Milyen t-próbáról van szó?
b) Egyetért vagy nem ért egyet a kutató következtetésével? Indokolja a választ.
=21.25