1.minta
2.minta
...
h.minta
1.elem
x
1,1x
2,1...
x
h,12.elem
x
1,2x
2,2x
h2...
...
...
...
...
i.elem
x
1,ix
2,ix
h,i...
...
...
...
...
utolsó elem
x
1, n1x
2,n2...
x
h,nhelemszámok
n
1n
2n
hátlagok
![]()
![]()
![]()
5.5. Több, normális eloszlású populáció középértékének összehasonlítása
Több független csoport középértékének összehasonlításakor nem alkalmas a kétmintás t-próba páronkénti alkalmazása
1. A fenti állítás indokolására elõször tekintsük a következõ példát. A kísérleti állatokat véletlenszerûen 3, egyenként 10 elemû csoportba osztották, az elsõ csoport nem kapott semmit, a másik két csoportot két különbözõ hormonnal kezelték. Vizsgálták mindegyiknek mindegyiktõl való eltérését. Az átlagra és szórásra következõ értékeket kapták:
|
A. Kontroll |
B. Testosteron |
C. Oestrogen |
|
|
elemszám |
10 |
10 |
10 |
|
átlag |
41.5 |
36 |
40 |
|
szórás |
3.8 |
5 |
5 |
Ha páronként elvégezzük a kétmintás t-próbát, a következõ t-értékeket kapjuk:
A-B: t=2.39 A-C: t=0.93 B-C: t=1.34
Mivel a szabadságfok mindhárom esetben 8, a p=0.05 esetén a kritikus t-érték t
krit=2.101. Így csak az A és B közötti különbság szignifikáns 95 %-os szinten, és így azt a látszólagos ellentmondást kapjuk, hogy bár sem az A sem a B csoport nem különbözik C-tõl, egymástól különböznek. A t-próba páronkénti alkalmazásából fakadó ilyen ellentmondás még feloldható: a különbség megállapításánál is elkövettünk 5% hibát, a "nincs különbség" megállapítása pedig nem jelent egyenlõséget.2. A fenti probléma tehát feloldható. Van azonban a páronkénti t-próba több csoportra történõ alkalmazásával kapcsolatban egy komolyabb probléma is. Ha a három csoportot külön-külön teszteljük páronként, A-B hasonlításakor, ha a különbség szignifikáns, a hibánk valószínûsége 0.05. A hiba elkerülésének valószínûsége 1-0.05=0.95. Hasonlóan az A-C és B-C hasonlításánál. Ha a három csoportot közösen teszteljük, és azt akarjuk állítani, hogy legalább 1 pár különbözik (0.05 hibavalószínûséggel), a hiba elkerülésének valószínûsége 0.95*0.95*0.95=0.857375, a hiba valószínûsége tehát 1-0.857375=0.142625, körülbelül tehát 0.15 is lehet a hibánk valószínûsége.
3 Tegyük fel, hogy 12 csoportunk van, és szeretnénk meghatározni a köztük levõ különbségeket. Ehhez 12*11/2=66 összehasonlítás szükséges. Ha az összehasonlítások függetlenek (ami nem is mindig igaz), az elsõ fajta hiba elkerülésének valószínûsége 0.95
66, , ami kb. =0.03. A hiba valószínûsége tehát 1-0.03=0.97. Általában, n számú független összehasonlítás esetén annak valószínûsége, hogy legalább egy összehasonlítás hibás (legalább egyszer elkövetjük az elsõ fajta hibát), maximum: 1-(1-a )n .Bebizonyítható, hogy a kétmintás-t-próba páronkénti alkalmazásánál sok minta esetén nagy a valószínûsége, hogy szignifikáns különbséget kapunk még egy és ugyanazon eloszlásból származó minták esetén is. Véletlen minta generálásával szimulációs kísérlettel magunk is meggyõzõdhetünk róla.
Általában is igaz, hogy ha a kísérletünk több változót eredményez, akkor a két minta összehasonlítására vonatkozó módszerek páronkénti alkalmazása nem megfelelõ.
A variancia analízis
A variancia analízis sokféle kísérleti elrendezésbõl származó minták középértékeinek összehasonlítására való kiértékelési módszer. Mi a legegyszerûbb esetben mutatjuk be az analízist: az ún. egyszempontos variancia analízis esetén, több független minta összehasonlítását.
Egyszempontos variancia-analízis : több független, normális eloszlású populáció középértékének összehasonlítása
Az egyszempontos variancia-analízis a kétmintás t-próba általánosítása több független csoport esetére, tehát a várható értékeket hasonlítja össze, mégpedig a teljes variancia felbontásával. Ezért hívják variancia-analízisnek (ANOVA - Analysis of Variance).
Legyen adott: h számú minta, jelölje n
i az i-edik minta elemszámát, yij a i-edik minta j-edik elemét, ahogyan azt a táblázat mutatja.Legyen adott: h számú minta, jelöle n
j a j-edik minta elemszámát, xij a j-edik minta i-edik elemét, ahogyan azt a táblázat mutatja:
|
1.minta |
2.minta |
... |
h.minta |
|
|
1.elem |
x 1,1 |
x 2,1 |
... |
x h,1 |
|
2.elem |
x 1,2 |
x 2,2 |
x h2 |
|
|
... |
... |
... |
... |
... |
|
i.elem |
x 1,i |
x 2,i |
x h,i |
|
|
... |
... |
... |
... |
... |
|
utolsó elem |
x 1, n1 |
x 2,n2 |
... |
x h,nh |
|
elemszámok |
n 1 |
n 2 |
n h |
|
|
átlagok |
|
|
|
Feltevés: mindegyik minta normális eloszlású, azonos szórású populációból származik, aza a j-edik minta N(m
j,s ) eloszlásból. A nullhipotézis és az alternatív hipotézis a következõ:H
0: m 1 = m 2 = ... = m h , azaz a vizsgált populációk átlagai megegyeznek, a minták egy és ugyanazom populációból származnak.H
a:Módszer: a varianciát kétféleképpen is kiszámoljuk, az egyik a mintákon belüli, a másik a minták közötti variancia becslése. Ha igaz H0, akkor mindkét módon ugyanazt a varianciát becsültük, tehát a varianciáknak egyenlõknek kell lenniük, így az elõzõ nullhipotézis helyett a következõt teszteljük:
H
0': s2között = s2belülH
a': s2között > s2belülA mintákon belüli
variancia becslése az egyes varianciák "súlyozott" átlaga:![]()
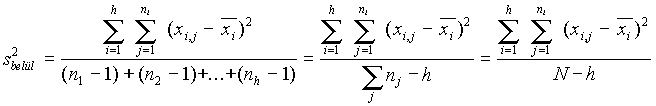
Ez a varianciának akkor is jó becslése, ha az átlagok nem egyenlõk . (Nevezhetjük hibavarianciának vagy nem magyarázott varianciának is)
A minták közötti variancia becsléséhez kiszámoljuk a minta-átlagokat, és ezeknek a varianciáját vesszük:
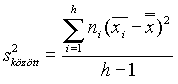
ahol 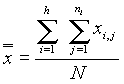 jelenti az összes adat átlagát, N pedig az össz-elemszámot.
jelenti az összes adat átlagát, N pedig az össz-elemszámot.
Ez a varianciának csak a nullhipotézis teljesülése esetén jó becslése, nevezhetjük magyarázott varianciának is.
Az összvariancia becslése pedig
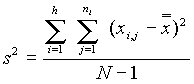
A nullhipotézis teszteléséhez a két varianciát kell összehasonlítanunk: a minták közötti variancia nagyobb-e, mint a mintákon belüli . ( Itt egyoldalú próbát végzünk, ha a minták közötti variancia kisebb, mint a mintákon belüli, máris megtartjuk H0-t). Két varianciát F-próbával hasonlítunk össze. Most
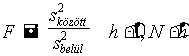 szabadságfokú F-eloszlású valószínûségi változó.
szabadságfokú F-eloszlású valószínûségi változó.
Ha F>Ftábla, elvetjük H0-t és azt mondjuk, hogy a minták közötti nagy varianciát a mintaátlagok közötti eltérés okozta, van tehát az átlagok között a többitõl különbözõ.
Ha F<Ftábla, akkor megtartjuk a nullhipotézist .
Azt, hogy a varianciákat kétféleképpen is fel tudtuk írni, a teljes eltérésnégyzetösszeg felbontásával szemléltethetõ. Ez egyúttal módot ad arra, hogy a variancia analízis számolását táblázatba foglaljuk.
A teljes eltérés-négyzetösszeg felbontása mintán belüli és minták közötti négyzetösszegekre.
Azt, hogy a varianciákat kétféleképpen is fel tudtuk írni, a teljes eltérés-négyzetösszeg felbontásával szemléltethetõ. A teljes variancia számlálóját átalakítjuk, hozzáadjuk és levonjuk ugyanazt a tagot:
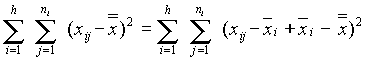
A jobboldalt két tagnak felfogva elvégezzük a négyzetreemelést:
A teljes eltérésnégyzetösszeg felbontása alapján a következõ tálázatot szokták megadni:
|
A szóródás oka |
Négyzetösszeg |
Szabadságfok |
Variancia |
F |
|
Minták között |
|
h-1 |
|
|
|
Mintákon belül |
|
N-h |
|
|
|
Teljes |
|
N-1 |
Specifikus kezelés-átlagok összehasonlításai
Többszörös (páronkénti) összehasonlítások, specifikus kezelés-átlagok összehasonlításai
Ha a variancia-analízis eredménye nem szignifikáns, akkor az analízisnek vége, és azt modjuk, hogy a várható értékek között nincs különbség.
Ha a variancia-analízis eredménye szignifikáns, akkor csak annyit mondhatunk, hogy a populációk átlagai között van legalább egy, a többitõl eltérõ. Azt, hogy melyik az, ahhoz páronként össze kell hasonlítanunk az átlagokat. Speciális próbákat dolgoztak ki, melyek többé-kevésbé mind az egész kísérletre vonatkozóan "garantálják", hogy az elsõ fajta hiba valószínûsége a , tehát adott szignifikancia szinten tarjták az elsõ fajta hiba valószínûségét. Ezek közül néhány:
1. t-próba (LSD-legkisebb szignifikáns differencia))
A t-próba képletét alkalmazza, csak most az összevont szórás helyébe a variancia-analízisbõl kapott sb-t teszi, így az i-edik és j-edik csoport közötti különbséget a következõ képlettel adott, N-h szabadságfokú t-próbával teszteli: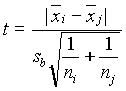 .
.
2. Bonferroni módszer
a t-próba képletét alkalmazzuk, de nem a , hanem a /c szinthez tartozó t-értékehez hasonlítjuk (kétoldali táblázat esetén) , ahol c az összehasonlítások száma. Ha a programrendszerek által kiadott p-értéket (Sig.level) használjuk, akkor a kétmintás t-hez tartozó p-értéket le kell osztani az összehasonlítások számával. Nyilvánvaló, hogy ez a módszer csak kisszámú összehasonlítás esetén alkalmazható inkább.
3. Sidak teszt : a fenti t-értéket számolja, de a helyett 1-(1-a )
1/(k(k-1)/2) szintet használ, a Bonferroni módszernél szûkebb határokat ad.4. Tukey-próba minden lehetséges, nagyszámú páronkénti hasonlítás esetén a Tukey próba rövidebb intervallumokat ad, mint a Scheffé vagy a Bonferroni (azaz hamarabb mutat szignifikáns eltérést). Képlete egyenlõ elemszám esetére
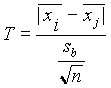
mennyiséget speciális táblázatból, az ún. studentizált terjedelmek táblázatából kell kikeresni (h, N-h) esetén.
6. Scheffé próba minden lehetséges kontrasztra vagy más lineáris hipotézisre, beleértve a páronkénti összehasonlításokat: két csoport akkor tekinthetõ szignifikánsan különbözõnek, ha
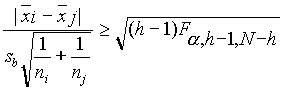
A kontraszt definíciója: ![]() , ahol az aj-k összege 0. Pld. m
1 és m
2 összehasonlítására vonatkozó kontraszt: 1×
m
, ahol az aj-k összege 0. Pld. m
1 és m
2 összehasonlítására vonatkozó kontraszt: 1×
m
1×
m
1+(-1/2)×
m
2+(-1/2)×
m
3. Ha pl. valamilyen kezelés utáni vizsgálat eredményei egy kezelés után 1, 2 ill. 3 óra múlva, akkor feladatunk lehet a csoportok várható értékei hasonló lineáris növekedést vagy csökkenést mutatnak. A feltevésünk így fogalmazható meg:![]()
7. Dunnett próba minden csoportot egyetlen csoporthoz (kontroll) hasonlít.
Mikor melyiket alkalmazzuk?
1. Minden lehetséges páronkénti hasonlítás esetén a Tukey próba rövidebb intervallumokat ad, mint a Scheffé vagy a Bonferroni (azaz hamarabb mutat szignifikáns eltérést)
2. Ha minden kontraszt is érdekel, a Scheffé a legjobb. Ha csak néhány, Bonferroni.
3. Tukey és Scheffé használhatók arra, hogy azt vizsgáljuk, amit az adatok szuggerálnak, a Bonferrori erre nem használható.
4. Számítsuk ki mindet, és a végén a számunkra legmegfelelõbbet használjuk.
A variancia analízis modelljei
Az elõbbiekben azt a legegyszerûbb esetet tárgyaltuk, amikor egy, az általunk vizsgált változó értékét csak egyféle "szempont" hatása (pl. különbözõ kezelések) befolyásolja. Ezért is hívják egyszempontos variancia analízisnek, és ezért van a teljes eltérés-négyzetösszeg csak két részre felbontva, egy kezelés (minták közötti) és egy hibatagra (mintákon belüli).
Ha a változónk értékét egy másik tényezõ is befolyásolja, akkor a teljes eltérésnégyzetösszeg több részre bontható fel, és külön vizsgálható a két szempont hatása. (Például kezelés és nemek szerinti különbségekre vagyunk kiváncsiak). Az ilyen analízist kétszempontos variancia analízisnek nevezzük.
Ha nem több, nem független változó középértékét szereténk összehasonlítani, megint félrevezetõ eredményeket adhat az egymintás t-próba többszöri alkalmazása. Ehelyett speciális variancia analízist, ún. ismételt méréses (repeated measures) variancia analízist kell alkamazni. Itt a kezelés-hatás mellett megjelenik az ismétlések hatása vagy blokkhatás is, és természetesen a hibatag.
Ezekkel a modellekkel nem foglalkozunk részletesen.
Példa. Egereken kísérleteztek: GdCl3 nevû szer hatását vizsgálva a fehérvérsejtszámra. Három kísérleti csoport volt: egy kontroll, és két módon beadott GdCl3: GdCl3-ip és GdCl3- iv. Kérdés, hogy a szernek volt-e hatása a fehérvérsjejtszám alakulására, és különbözõ volt-e a hatása a kétféle GdCl3 kezelés esetén. Erre a problémára alkalmazható az egyszempontos variancia-analízis.
Megjegyzés.
A futtatáshoz felhasznált adatok a SZOTE kutatásai során keletkeztek, az eredményeket már közöltük, bemutatásukhoz a társszerzõk hozzájárultak; a futtatási eredményeket felhasználói és oktatási szempontból szeretném értelmezni.
Az adatok beírása:
Eredeti adatok esetén az SPSS-ben két változót kell megadni: az egyik egy kategorikus numerikus változó (gdcl3), melybe a csoportok kódjait írjuk, a másik szintén numerikus változó (osszfvs), melybe az összfehérvérsejtszámokat írtuk be. A kódokat célszerû egymást követõ számok formájában megadni, és alkalmazni a "Value Label" -t a kódokra. Mi a következõ kódokat alkalmaztuk: 0-kontroll, 1 - GdCl3 ip, 2 -GdCl3-iv.
Az egyszempontos variancia-analízis futtatása SPSS-ben: válasszuk a Statistics menüben a Compare Means almenüjében a One-Way Anova pontot. Az itt megjelenõ ablakokba a következõket kell beírni:
Dependent List: ide kell írni azt a változót, amelynek az átlagait össze szeretnénk hasonlítani (lehet többet is) (osszfvs)
Factor: a csoportok kódjait tartalmazó változó, ugyanaz, ami a kétmintás t esetén a Grouping Variable, vagy a Means-nél az Independent List (gdcl3)
Define Range: A két kérdõjel azt jelzi, hogy be kell írnunk a csoportosító változó azon értékeit, amelyek szerinti csoportokat össze szeretnénk hasonlítani. Ez az opció az SPSS 7.5-ben már nem szerepel.
Contrasts: itt lehet megadni a tesztelni kívánt kontrasztokat, az együtthatók megadásával.
Post Hoc: ha páronkénti hasonlításokat szeretnénk, akkor itt kell bejelölni, hogy melyik fajtát kérjük (LSD, Bonferroni, Scheffé, stb.).
Options:
Descriptive: az egyes csoportok átlagait és szórásait lehet kiíratni. Ha nem jelöljük be, nem írja ki.
Homogeneity-of-variance: a variancia-analízis egyik feltételét, a varianciák egyezését vizsgálja, ha ezt az opciót bejelöljük.
A ONEWAY eljárás egyéb lehetõségei SPSS 6.1-ben
Adott átlagok, standard deviációk és az elemszámok esetén is futtatható az egyszempontos ANOVA, de ebben az esetben a parancs szintaxist kell használni, hogy hogyan, az a Syntax Reference-ben megtalálható.
Eredmények.
A variancia-analízist az eredeti adatok logaritmusán végezzük el, mivel az eredeti adatok varianciái különböznek, mégpedig nagyobb átlaghoz nagyobb szórás tartozik.
Variable LNFVS
By Variable GDCL3
Analysis of Variance
Sum of Mean F F
Source D.F. Squares Squares Ratio Prob.
Between Groups 2 9.7554 4.8777 19.0953 .0000
Within Groups 26 6.6414 .2554
Total 28 16.3968
Standard Standard
Group Count Mean Deviation Error 95 Pct Conf Int for Mean
Grp 0 17 14.8837 .5233 .1269 14.6146 TO 15.1527
Grp 1 6 16.1187 .5224 .2133 15.5704 TO 16.6670
Grp 2 6 14.4130 .4233 .1728 13.9688 TO 14.8573
Total 29 15.0418 .7652 .1421 14.7507 TO 15.3329
GROUP MINIMUM MAXIMUM
Grp 0 13.8499 15.6718
Grp 1 15.4677 16.6959
Grp 2 13.8791 15.0440
TOTAL 13.8499 16.6959
Levene Test for Homogeneity of Variances
Statistic df1 df2 2-tail Sig.
.4378 2 26 .650
Multiple Range Tests: Scheffe test with significance level .05
The difference between two means is significant if
MEAN(J)-MEAN(I) >= .3574 * RANGE * SQRT(1/N(I) + 1/N(J))
with the following value(s) for RANGE: 3.67
(*) Indicates significant differences which are shown in the lower triangle
G G G
r r r
p p p
2 0 1
Mean GDCL3
14.4130 Grp 2
14.8837 Grp 0
16.1187 Grp 1 * *
A variancia-analízis feltételei közül a varianciák azonosságát a Levene teszttel ellenõriztük. Látható, hogy a p-érték 0.650, nem szignifikáns, így a varianciák azonosságára vonatkozó nullhipotézist elfogadjuk.
A kísérleti csoportok átlagaira vonatkozó összehasonlítás eredményeként az ANOVA táblázatban F=19.095, (2,26) szabadságfokokkal, a Sig mezõben 0.000 áll, azaz p<0.0001, tehát a kezelt és a kontroll csoportok között van szignifikáns különbség. A páronkénti hasonlítások eredményeképpen látható, hogy a GdCl3-ip csoport átlaga szignifikánsan különbözik mind a kontrolltól, mind a GdCl3-iv csoporttól.