5.6. Két mennyiség kapcsolatának vizsgálata, korreláció és lineáris regresszió
Gyakran elõfordul, hogy két változó mennyiség közötti kapcsolatot vizsgálunk. A kapcsolat szorosságát célszerû egy mérõszámmal jellemezni. Nagyon sok ilyen mérõszám létezik, ezek közül a legelterjedtebb az ún. korrelációs együttható, vagy Pearson-féle korrelációs együttható. (Karl Pearson, 1857-1936). Az együtthatót r-rel jelöljük, és a mérések közötti lineáris kapcsolat szorosságát méri.
Hogy mit jelent a lineáris kapcsolat és hogy ezt r hogyan tudja mérni, tekintsünk egy példát. Szemléltetésképpen csak 6 elemû mintát mutatunk be. 6 hallgatónak mérték az adás-vétel, a színház, a matematika és a nyelvek iránti érdeklõdését. Az alábbi eredményeket kapták:
|
hallgató |
adás-vétel iránti érdeklõdés |
színház iránti érdeklõdés |
matematika iránti érdeklõdés |
nyelvek iránti érdeklõdés |
|
Pat |
51 |
30 |
525 |
550 |
|
Sue |
55 |
60 |
515 |
535 |
|
Inez |
58 |
90 |
510 |
535 |
|
Amie |
63 |
50 |
495 |
520 |
|
Gene |
85 |
30 |
430 |
455 |
|
Bob |
95 |
90 |
400 |
420 |
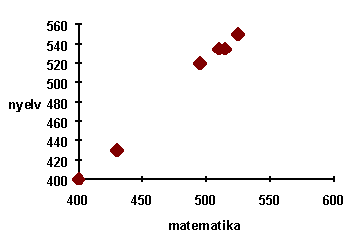
Tekintsük például a mamatematika és a nyelvek iránti érdeklõdés közötti kapcsolatot. Ehhez egy ún. szóródási diagramot készítünk: az x tengelyt használjuk a matematika, az y tengelyt a nyelvek iránti érdeklõdés megjelölésére. Ebben a koordináta rendszerben így minden hallgatóhoz egy pont fog tartozni. Használhattuk volna a tengelyeket fordítva is, mivel nem az egyik változónak a másiktól való függését, csak a kapcsolatukat nézzük.
A szóródási diagramon a következõket vehetjük észre:
1. Minden érték-párhoz egy pont tartozik, esetünkben 6 pont van.
2. A pontok közelítõleg egy egyenes mentén helyezkednek el. Ha ilyen a pontok elhelyezkedése, akkor azt mondjuk, hogy a változók között jó a korreláció.
3. Nagyobb matematika-értékekhez nagyobb színház-értékek tartoznak, tehát az egyenes növekvõ. Ilyen esetben a korrelációt pozitívnak mondjuk.
Most tekintsük a matematika és a színház iránti érdeklõdés közötti kapcsolatot. Látható, hogy a pontok szóródnak, semmilyen egyenes mentén nem látszanak elhelyezkedni, Ilyenkor azt mondjuk, hogy a változók között nincs korreláció, nincs lineáris kapcsolat.
Megjegyezzük, hogy nem szükséges mindkét változót azonos léptékû tengelyeken ábrázolni, mivel a pontok egymáshoz viszonyított elhelyezkedése érdekel, nem az aktuális értékük.


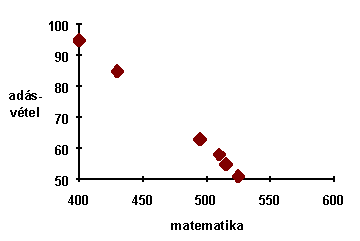
A matematika és az adás-vétel közötti értékek közötti kapcsolatnál látható, hogy a pontok egy csökkenõ egyenes mentén helyezkednek el. Ilyenkor azt mondjuk, hogy a változók között negatív korreláció van.
A korrelációs együttható ( r) számítása
Jelölje a két változóra vett mintát ![]() .
.
Ekkor a korrelációs koefficiens a következõ képlet szerint számítható ki:
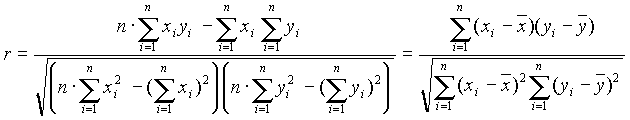
A korrelációs együttható tulajdonságai
r mindig -1 és 1 között van.
Ha a pontok nem fekszenek egy egyenes mentén, akkor azt mondjuk, hogy nincs korreláció közöttük (r=0), vagy gyenge korreláció van közöttük ( r közel van 0-hoz.). Ha a pontok egy egyenes mentén fekszenek, akkor r közel van +1-hez vagy -1-hez, ekkor azt mondjuk, hogy a két változó között szoros vagy magas korreláció van. Ha a pontok pontosan rajta vannak egy növekvõ egyenesen, akkor r=1, ha pedig egy csökkenõ egyenesen vannak pontosan rajta, akkor r=-1.
Teszt a korrelációs együttható szignifikanciájára
Tegyük fel, hogy egy populáció vizsgálata során ki tudtuk számítani a populációbeli korrelációs együtthatót két változó közötti lineáris kapcsolat mérésére. Ha ez az együttható 0 lenne, azt moshatnánk, hogy nincs korreláció a két változó között. Tehát, ha egy mintát vizsgálunk, akkor a mintából számított korrelációs együttható 0-hoz közeli értéke arra enged következtetni, hogy nincs korreláció a két változó között. 0-tól távol esõ (1-hez vagy -1-hez közeli) értékek pedig bizonyos korreláció meglétére engednek következtetni. A statisztikai szempontból el kell tudnunk dönteni, hogy r értéke elég messze van-e 0-tól ahhoz, hogy elég nagy biztonsággal állíthassuk, hogy valóban fennáll.
H0: korrelációs együttható a populációban = 0, jelölésekkel r =0
Ha: ![]()
Ez a próba egy t eloszlású statisztikával hajtható végre. Bebizonyítható, hogy ha igaz a nullhipotézis, a következõ, t-vel jelölt statisztika
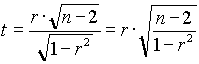
t-eloszlású n-2 szabadságfokkal.
Döntés statisztikai táblázat használatával: ha ttable jelöli az n-1 szabadságfokhoz és a valószínûséghez tartozó táblabeli értéket, akkor ha |t| > ttable, elvetjük H0 -t és azt mondjuk, hogy a populáció korrelációs együtthatója, r , különbözik 0-tól.
Döntés a p-értékek szerint: ha p < a , elvetjük H0 -t és azt monjuk, hogy a populáció korrelációs együtthatója, r , különbözik 0-tól.
Példa.
A matematika és a nyelvtudást felmérõ teszt változói közötti korrelációs együttható értéke 6 elemû mintából számolva r=0.9989.
H0: korrelációs együttható a populációban = 0, jelölésekkel r =0.
Ha: korrelációs együttható a populációban különbözik 0-tól.
Számítsuk ki a t-statisztikát 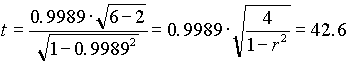
A táblabeli kritikus érték t0.05, 4 = 2.776. Mivel 42.6 > 2.776, elvetjük H0 -at és azt állítjuk, hogy a két változó, a matematika és a nyelvtudás közötti korreláció szignifikánsan eltér 0-tól 95 % -os szinten.
Lineáris regresszó
Ha két változó kapcsolatának vizsgálatakor magas korrelációt kapunk, megpróbálhatjuk az összefüggést egy ideális egyenessel jellemezni - egy olyan egyenessel, amely a legjobban reprezentálja a lineáris kapcsolatot. Ekkor felírhatjuk az egyenes egyenletét, és ezt használhatjuk pl. arra, hogy "megjósoljuk" egy adott x értékhez az "ideális" y-t.
Például, tegyük fel, hogy a matematika tudást és a nyelvtudást felmérõ teszt pontszámain magas korrelációt kaptunk ( r =0,9989). Ha az ideális egyenes egyenlete nyelvtudás = 1.016 matematika + 15.5, akkor 410-es matematika pontszámhoz a formula a 432 "ideális" nyelvtudás pontszámot rendeli.
Nyilván, ha 10 hallgatónak lenne 410 pontja matematikából, nem várjuk, hogy mind a 10-nek 432 pontja legyen nyelvbõl is. Még az is elõfordulhat, hogy egyiknek sem lesz pontosan 432 pontja nyelvbõl. Ez a formula csak azt állítja, hogy a 10 hallgató átlagának a legjobb becslése a 432.
Megjegyzés: Vegyük észre, hogy az elõbbi szituáció értelmezése semmit nem mond a korreláció okáról, a teszt kérdések jellegérõl, a hallgatók intelligenciájáról. A korreláció fennállása csak annyit jelent, hogy ez a lineáris kapcsolat létezik a két változó között, és ha a populáció, amelybõl a mintát vettük, ugyanaz, akkor valószínû, hogy használható a regressziós egyenes adott matematika pontszámból a nyelv pontszámára vonatkozó következtetés levonására.
A legjobban illeszkedõ egyenes meghatározása
Az egyenes egyenletének általános alakja y = a + b x. Szeretnénk meghatározni a és b értékét úgy, hogy az egyenes a legjobban illeszkedjen a pontokra. Tegyük fel, hogy n számú megfigyelés párunk van: (xi, yi) , i=1,2,...,n. Szeretnénk yi -t az egyenes xi helyen felvett értékeivel közelíteni, azaz a + b xi -vel.
A közelítés akkor jó, ha az ![]() különbségek kicsik, Mivel ezek a különbségek pozítívak és negatívak is lehetnek, vegyük ezek négyzetét és összegezzük a különbségek négyzetét. Így a következõ összeget kapjuk, melyet minimalizálnunk kell:
különbségek kicsik, Mivel ezek a különbségek pozítívak és negatívak is lehetnek, vegyük ezek négyzetét és összegezzük a különbségek négyzetét. Így a következõ összeget kapjuk, melyet minimalizálnunk kell:
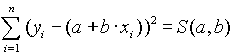
Ebben az összegben a és b az ismeretlen, mivel az (xi, yi) párok most a mérési értékeket jelölik, tehát ezek adott számok. A fenti összeg tehát az a és b függvénye. Szokták a reziduálok négyzetösszegének vagy eltérés-négyzetösszegnek is nevezni. a és b meghatározásához az S(a,b) függvény minimumát kell meghatároznunk. Ez egy kétváltozós függvény, szélsõ értékeinek megtalálásához az elsõ deriváltakat nullával kell egyenlõvé tenni és megoldani az egyenletrendszert, azaz
![]()
Az egyenletrendszer megoldása a-ra és b-re :
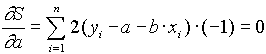
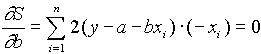
A beszorzás után kapjuk:
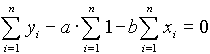
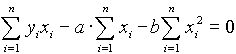
Az elsõ egyenletet ![]() -nel beszorozva kapjuk:
-nel beszorozva kapjuk:
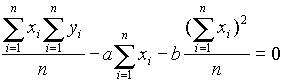
a második egyenletbõl e fentit kivonjuk:
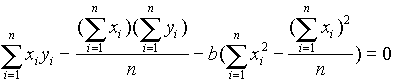
Innen b-t ki lehet fejezni:
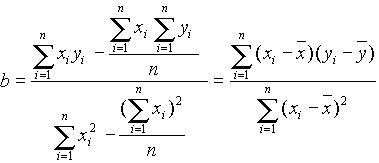 és
és ![]()
Bebizonyítható a második deriváltakkal, hogy ezek a helyek valóban minimumhelyek.
a és b geometriai jelentése.
a: regressziós együtthatónak nevezzük, és a (legjobban illeszkedõ) regressziós egyenes meredeksége;
b: a regressziós egyenes y-tengelymetszete.
A korrelációs együttható kiszámítása a regressziós együttható segítségével.
A korrelációs és regressziós együttható között fennáll a következõ összefüggés:
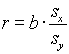 , ahol sx, sy az x1, x2,...,xn és y1, y2,...,yn.minták standard deviációi. Ebbõl a formulából látható, hogy r és b elõjele megegyezik, mivel a standard deviáció mindig pozitív. Tehát negatív korreláció esetén a regressziós egyenes meredeksége negatív és fordítva. Bebizonyítható, hogy ugyanaz a t-próba alkalmazható a regressziós együttható nullától való eltérésének szinifikanciájára, mint a korreláció szignifikanciájának vizsgálatára.
, ahol sx, sy az x1, x2,...,xn és y1, y2,...,yn.minták standard deviációi. Ebbõl a formulából látható, hogy r és b elõjele megegyezik, mivel a standard deviáció mindig pozitív. Tehát negatív korreláció esetén a regressziós egyenes meredeksége negatív és fordítva. Bebizonyítható, hogy ugyanaz a t-próba alkalmazható a regressziós együttható nullától való eltérésének szinifikanciájára, mint a korreláció szignifikanciájának vizsgálatára.
Korrelációs együttható és determinációs együttható.
Tegyük fel, hogy van n számú megfigyelésünk az Y változóra, de nincs hozzá megfigyelésünk az X független változóra. Ilyen esetben az yi "ideális" értéke az yi-k átlaga: 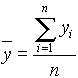 . A becslés hibája
. A becslés hibája ![]() .
.
Mégis, ha rendelkezésre állnak az X független változóra vonatkozó megfigyelések is, akkor ezeket is használhatjuk az yi-k "ideális" értékánek meghatározásához, mégpedig a regressziós egyenes segítségével. Az "ideális" érték ![]() . lesz, a becslés hibája pedig
. lesz, a becslés hibája pedig ![]() .
.
A két hibatag különbségét véve kapjuk:
![]()
Tehát, egy független változó kapcsolatát felhasználva a becslés hibáját egy ![]() taggal (amely mindig pozitív) csökkentettük. Bebizonyítható, hogy általában hasonló összefüggés igaz az eltérésnégyzet-összegekre is:
taggal (amely mindig pozitív) csökkentettük. Bebizonyítható, hogy általában hasonló összefüggés igaz az eltérésnégyzet-összegekre is:
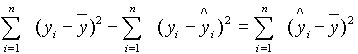
Itt az elsõ tag a teljes variancia képletének számlálója, a másodikban a reziduálok négyzetösszege van, szokás a regresszió által nem magyarázott tagnak vagy hibatagnak is nevezni, a jobboldal pedig a regresszió által magyarázott tag. Tehát a fenti négyzetösszegek szavakkal így írhatók le
"Teljes" - "Hiba" = "Magyarázott"
Ha a "Teljes"-t kifejezzük
"Teljes" = "Magyarázott" +"Hiba".
Bebizonyítható, hogy a magyarázott és a teljes eltérés-négyzetösszeg hányadosa éppen a korrelációs együttható négyzete:
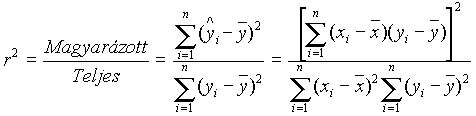
A korrelációs együttható négyzetét determinációs együtthatónak nevezzük. Általában 100-zal megszorozzuk, hogy % jelentése legyen. Jelentése: az Y összvarianciájának hány százaléka magyarázható a regresszióval.
Példa.
A nyelvtudás és a matematika tudás közötti korreláció vizsgálatakor r =0,9989-et kaptunk a korrelációra. A determinációs együttható, r2 = 0.917 . Tehát a nyelvtudás összvarianciájának 91.7% -a az õ matematika-tudással való lineáris kapcsolatával magyarázható, a maradék 8.3 % pedig a véletlen hiba.
Lineáris regresszió transzformációkkal
Idáig lineáris modelleket tanulmányoztunk, amikor az X és Y változók közötti kapcsolatot
y=a +b x
alakban kerestük. Ez a modell az a és b paramétrekben lineáris.
Néha a modellek nem lineárisak. Ha elkészítjük az két változó szóródási diagramját ( a koordináta rendszerbe berajzoljuk az (xi, yi) pontpárokat), a pontok valamely nemlineáris görbe mentén helyezkednek el. Speciális esetekben meg tudjuk találni ezekhez a pontokhoz is a legjobban illeszkedõ függvényt.
Például. az
y=a (bx)
nem lineáris, mert az x változó a kitevõben van. Ahhoz, hogy a lineáris regressziós technikát alkalmazni tudjuk, a nemlineáris modellt lineárisba kell transzformálnunk, például vegyük mindkét oldal logaritmusát. 10-es vagy e alapú logaritmust is vehetünk. Ha a>0 és b>0, az
y=a (bx)
alakú modellbõl
log y = log a + x log b
alakot kapjuk. Jelölje Y=log y és A = log a és B = log b, akkor a modell transzformáció utáni alakja már lineáris.
Y=A + B x
Tehát, ha a függõ változó logaritmusát vesszük, a lineáris regresszióval meghatározhatjuk A -t és B-t, majd ezeket visszatranszformálva a-t és b-t.
Példa
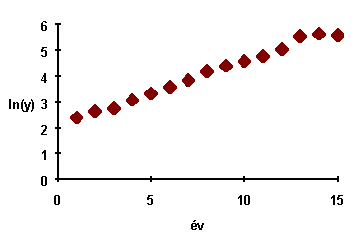
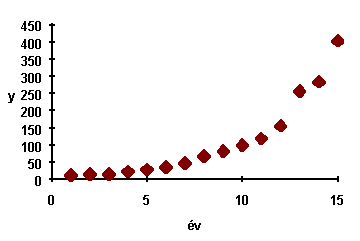
Wild Bill's Steakhouses, egy gyors-éttermi hálózat, 1974-ben indult. 1974-tól 1988-ig minden évben feljegyezték a mûködõ éttermek számát, yi -t. Az adatokat a táblázat szemlélteti. Egy elemzõ jellemezni akarta a társaság növekedését, Az eredeti adatok szóródási diagramja (bal oldali ábra) azt sejteti, hogy az x (év) és az y ( éttermek száma) közötti kapcsolatot egy exponenciális függvénnyel lehetne jellemezni. Az y-ok logaritmusait véve lineáris kapcsolatot kapunk (jobboldali ábra)
|
Year |
i |
y i |
ln y i |
Year |
i |
y i |
ln y i |
|
|
1974 |
0 |
11 |
2.398 |
1982 |
8 |
82 |
4.407 |
|
|
1975 |
1 |
14 |
2.639 |
1983 |
9 |
99 |
4.595 |
|
|
1976 |
2 |
16 |
2.773 |
1984 |
10 |
119 |
4.779 |
|
|
1977 |
3 |
22 |
3.091 |
1985 |
11 |
156 |
5.05 |
|
|
1978 |
4 |
28 |
3.332 |
1986 |
12 |
257 |
5.549 |
|
|
1979 |
5 |
36 |
3.584 |
1987 |
13 |
284 |
5.649 |
|
|
1980 |
6 |
46 |
3.829 |
1988 |
14 |
403 |
5.999 |
|
|
1981 |
7 |
67 |
4.205 |
A lineáris regressziót x és log (y)-on végrehajtva kapjuk:
log y = 2.327 + 0.2569 x
Tehát, y-t kifejezve
y = e
2.327 + 0.2569 x = e2.327 e0.2569 x= 1.293 e0.2569 x a legjobban illeszkedõ görbe egyenlete az eredeti adatokra.nEgy másik nemlineáris, de linearizálható modell :
y=a x
bMost mindkét oldal logaritmusát véve a köv. egyenletet kapjuk
log y = log a + b log x
Jelölje Y= log y, A= log a, X = log x, kapjuk, hogy
Y = A + B X
amely már lineáris függvény. Ha a szóródási diagram megfigyelésekor azt tapasztaljuk, hogy az adatok valamely hatványfüggvény mentén látszanak szóródni, akkor az y=a x
b modell alkalmazható úgy, hogy mindkét változó logaritmusát vesszük, és így ezeken végezzük el a regressziós analízist, majd a kapott A értéket visszatranszformáljuk.Néha a diagram reciprokos összefüggést sejtet. Ilyenkor x, y, vagy mindkettõ reciprokát véve kapjuk a alkalmazhatjuk a lineáris regressziót.
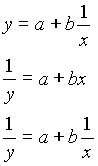
Chi-négyzet próbák
Függetlenségvizsgálat
Tekintsünk elõször egy példát. Tegyük fel, hogy véletlenszerûen megkérdeztek 200 embert, 50 férfit és 150 nõt arról, hogy mi a véleményük a gyógyszerek ellenõrizetlen szedésérõl. 60-an értettek egyet, 100-an voltak ellene, és 40-en közömbösek voltak. Ezeket az eredményeket egy táblázatban lehet összegezni, az úgynevezett gyakorisági vagy kontingencia táblázatban.
|
férfiak |
nõk |
sor összegek |
|
|
egyetért |
60 |
||
|
nem ért egyet |
100 |
||
|
tartózkodik |
40 |
||
|
oszlop-összegek |
50 |
150 |
200 = minta-elemszám |
Ha a vélemény független a nemtõl, a férfiak és nõk azonos arányban kell, hogy egyetértsenek, vagy ellenezzék a gyógyszerszedést. A 200 megkérdezett ember közül 60 értett egyet, az 30 %. Tehát, a férfiak és nõk 30 %-a ;értene egyet várhatóan a gyógyszerszedéssel. Az így kiszámított gyakoriságokat várható gyakoriságoknak nevezzük, tehát olyan gyakoriságoknak, melyet függetlenség esetén várunk. A következõ táblázat mutatja a várható gyakoriságok számítási módját cellánként:
|
férfiak |
nõk |
sor összegek |
|
|
egyetért |
60/200 az 50-bõl |
60/200 a 150-bõl |
60 |
|
nem ért egyet |
100/200 az 50-bõl |
100/200 a 150-bõl |
100 |
|
tartózkodik |
40/200 az 50-bõl |
40/200 a 150-bõl |
40 |
|
oszlop-összegek |
50 |
150 |
200 = minta-elemszám |
Látható, hogy a várt gyakoriságokat úgy lehet kiszámítani, hogy a megfelelõ sor- és oszlopösszegeket összeszorozzuk, és osztjuk a minta-elemszámmal. A számítás eredményét a következõ táblázat mutatja:
Várható gyakoriságok:
|
férfiak |
nõk |
sor összegek |
|
|
egyetért |
15 |
45 |
60 |
|
nem ért egyet |
25 |
75 |
100 |
|
tartózkodik |
10 |
30 |
40 |
|
oszlop-összegek |
50 |
150 |
200 = minta-elemszám |
Általában, a várható gyakoriságokat a következõ formula szerint számítjuk:
![]()
Ezek után a kísérletet elvégezve valójában a következõ gyakoriságokat kapták:
Megfigyelt (kapott ) gyakoriságok
|
férfiak |
nõk |
sor összegek |
|
|
egyetért |
17 |
43 |
60 |
|
nem ért egyet |
22 |
78 |
100 |
|
tartózkodik |
11 |
29 |
40 |
|
oszlop-összegek |
50 |
150 |
200 = minta-elemszám |
Vizsgáljuk meg a megfigyelt (O) és a várható (E) gyakoriságok különbségét: 2,-2,-3,3,1 -1. Nagyok vagy kicsik ezek a különbségek? Egy olyan számot (statisztikát) keresünk, amellyel ezt lehet tesztelni. A következõ táblázat ennek a számnak a képzését mutatja be.
|
cella |
Kategória |
megfigyelt(O) |
várt |
különbség |
a különbség négyzete |
az eltérésnégyzeteknek a várt gyakoriságokhoz viszonyított aránya |
|
1 |
férfiak mellette |
17 |
15 |
2 |
4 |
4/15=0.27 |
|
2 |
nõk mellette |
43 |
45 |
-2 |
4 |
4/45=0.09 |
|
3 |
férfiak ellene |
22 |
25 |
-3 |
9 |
9/25=0.36 |
|
4 |
nõk ellene |
78 |
75 |
3 |
9 |
9/75=0.12 |
|
5 |
férfiak vélemény nélkül |
11 |
10 |
1 |
1 |
1/10=0.1 |
|
6 |
nõk vélemény nélkül |
29 |
30 |
-1 |
1 |
1/30=0.03 |
|
összeg=0.97 |
A keresett számot c 2-tel jelöljük, és úgy lehet kiszámítani, hogy az utolsó oszlop elemeit összeadjuk. Formálisan:
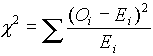 , ez tehát esetünkben egyenlõ 0.97.
, ez tehát esetünkben egyenlõ 0.97.
Ha nincs kapcsolat a változók között, azaz ha a két változó független, akkor a különbségek közel lesznek 0-hoz, így c 2 is közel lesz 0-hoz. Másrészt, ha c 2 messze van 0-tól, nagy a valószínûsége, hogy a változók nem függetlenek. Az ilyen típusú chi-négyzet próbáknál a nullhipotézis a változók függetlensége, azaz:
H0: a vélemények függetlenek a nemtõl.
Ha: a vélemények nem függetlenek a nemtõl.
Ahogyan ezt a t-eloszlás esetén is tettük, az általunk számolt értéket össze kell hasonlítani egy táblabeli értékkel. A c 2 eloszlás elméleti értékei szabadságfokok szerint rendezve táblázatokban találhatók. A szbadságfok 3 x2 -es táblázat esetén 2.
A szabadságfok számítása általában:
szabadságfok=(sorok száma -1) (oszlopok száma -1
Függetlenségvizsgálat általános esetben
Tegyük fel, hogy n számú kísérletet végeztünk, melynek eredményei két változó, X és Y értékeivel jellemezhetõk. Feltesszük, hogy X és Y diszkrét valószínûségi változók, lehetséges értékeiket jelölje x
1, x2,...,xr és y1, y2,...,ys , melyek az A1,A2,...,Ar és B1, B2,...,Bs események kimenetelei. Jelölje kij az (Ai, Bj) együttes bekövetkezésének gyakoriságát. Ezek a számok egy táblázatba rendezhetõk, melyet gyakorisági táblázatnak vagy kontingencia táblázatnak nevezünk. Ebben a táblázatban a köv. jelöléseket alkalmazzuk:
|
B 1 |
B 2 |
... |
B s |
Összeg |
|
|
A 1 |
k 11 |
k 12 |
... |
k 1s |
k 1. |
|
A 2 |
k 21 |
k 22 |
... |
k 2s |
k 2. |
|
... |
... |
... |
... |
... |
... |
|
A r |
k r1 |
k r2 |
... |
k rs |
k r. |
|
Összeg |
k .1 |
k .2 |
... |
k .s |
n |
Itt, 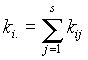 az A
az A
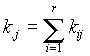 a Bj esemény gyakorisága. A két változó függetlensége az Ai és Bj események függetlenségét jelenti, tehát a nullhipotézis:
a Bj esemény gyakorisága. A két változó függetlensége az Ai és Bj események függetlenségét jelenti, tehát a nullhipotézis: Nyilván k
ij -k a megfigyelt gyakoriságok, a várható gyakoriságok pedig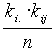 formula szerint számíthatók. A próbastatisztika:
formula szerint számíthatók. A próbastatisztika:
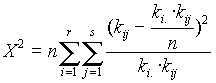
képlettel adott, és aszimptotikusan c 2 eloszlású (r-1)(s-1) szabadságfokkal.
Döntés: ha X
2 > c 2table , elvetjük anullhipotézist és azt mondjuk, hogy a két változó nem független, ellenkezõ esetben nem vetjük el a nullhipotézist.
Illeszkedésvizsgálat chi-négyzet próbával
Az illeszkedésvizsgálat célja annak meghatározása, hogy a mintaelemek adott eloszlású populációból származnak-e.
Tegyük fel, hogy adott egy X változóra vonatkozó statisztikai minta. Készítsünk hisztogramot a mintaelemekbõl. Jelölje a beosztások osztáspontjait c
0,c1,...,cr és az i-edik intervallumbe esés gyakoriságát ki (azoknak a mintaelemeknek a számát, amelyek a [ci-1,ci] intervallumba esnek) . Nyilván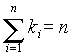 .
.
Azt a nullhipotézist szeretnénk tesztelni, hogy a minta adott eloszlású populációból származik. A nullhipotézis: H
0: X változó eloszlása adott eloszlás.Jelölje p
1,...,pr az intervallumokba esés valószínûségeit az adott eloszlás fennállása esetén.Ha ezek a valószínûségek ismertek, tiszta illeszkedésvizsgálatról beszélünk. Ha H
0 igaz és n nagy, akkor a ki/n relativ gyakoriságok a pi-k közelítései,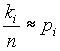 vagy
vagy ![]() , tehát az np
, tehát az np
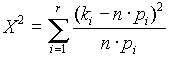 formulával adott, és c
2 eloszlású r-1 szabadságfokkal.
formulával adott, és c
2 eloszlású r-1 szabadságfokkal.
A következõkben megmutatjuk, hogyan alkalmazható a chi-négyzet próba egyenletes eloszlásra történõ illeszkedés tesztelésére.
Egyenletes eloszlásra történõ illeszkedésvizsgálat
Példa.
Kockajáték közben felmerül a gyanú, hogy szabályos-e a kocka. Kísérletképpen 120-szor feldobjuk a kockát. Ha szabályos, akkor minden dobás egyformán valószínû, tehát ideális esetben minden egyes számra 20-20 gyakoriságot várunk.
A kapott eredmények a következõk:
|
1 |
2 |
3 |
4 |
5 |
6 |
Összeg |
|
|
Eredmények |
24 |
15 |
15 |
19 |
25 |
22 |
120 |
H0: a kocka szabályos, a kimenetelek egyformán valószínûek
A megfigyelt (kapott) gyakoriságok tehát a fenti sorban vannak, a várható gyakoriságok (p
i-k) mindegyike adott (20).|
1 |
2 |
3 |
4 |
5 |
6 |
Összeg |
|
|
Megfigyelt gyakoriságok |
24 |
15 |
15 |
19 |
25 |
22 |
120 |
|
Várt gyakoriságok |
20 |
20 |
20 |
20 |
20 |
20 |
120 |
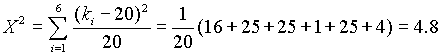
A szabadságfok 5, a táblabeli kritikus érték c
20.05,5=11.07.Mivel a mi próbastatisztikánk, 4.8 < 11.07 nem vetjül el H
0 -t, elfogadjuk, hogy a kocka szabályos (nincs elegendõ bizonyítékunk arra, hogy nem szabályos).Normalitás vizsgálat
A következõkben az ún. becsléses illeszkedésvizsgálatra mutatunk be példát. Normalitás vizsgálat esetén általában nem ismerjük az eloszlás paramétereit, ezért azokat a mintából kell becsülni. Ezek segítségével fogjuk a p
i-ket is megkapni. Innen az elnevezés.Tegyük fel, hogy van egy mintánk, melyrõl el szeretnénk dönteni, hogy normális eloszlású populációból származik-e. Készítsünk hisztogramot. A
H0: a minta normális eloszlású populációból származik,
hipotézis eldöntéséhez szükségünk van a várt gyakoriságokra. Ehhez elõször becsülnünk kell a normális eloszlás paramétereit az ![]() mintaátlaggal és az s standard deviációval . A p
mintaátlaggal és az s standard deviációval . A p
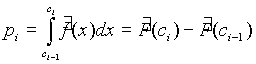 , ahol
, ahol 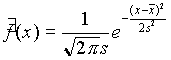 ,
,
formula direkt alkalmazásával nyerhetõk, a próbastatisztika
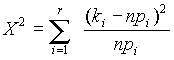 c
2 eloszlású r-2-1 szabadságfokkal (2 a paraméterek száma). Becsléses illeszkedésvizsgálatnál a szabadságfok r-s-1, ahol s az eloszlás paramétereinek száma.
c
2 eloszlású r-2-1 szabadságfokkal (2 a paraméterek száma). Becsléses illeszkedésvizsgálatnál a szabadságfok r-s-1, ahol s az eloszlás paramétereinek száma.
Gauss-papír alkalmazása
Van egy egyszerû grafikus módszer a normalitás vizsgálatra. A "Gauss-papír" speciális koordináta rendszer, amelyben az tengely beosztása a normális eloszlás inverzének megfelelõen van feltüntetve százalékokban. A minta eloszlásfüggvényét ebbe a rendszerbe belerajzolva normalitás esetén közelítõleg egy egyenest kapunk.
Nemparaméteres próbák
Az eddig alkalmazott próbák nagy részénél az alkalmazhatóság feltétele volt az, hogy ismerjük, hogy a minta milyen eloszlású populációból származik. A próba az eloszlás típusát ismertnek tételezve fel, az eloszlás egyes ismeretlen paramétereire tett hipotézisek ellenõrzésével foglalkoztak. Például, a t-próbák alkalmazásának egyik feltétele, hogy a minta(minták) normális eloszlású populációból származzon(anak), a hipotézis az eloszlás m paraméterére vonatkozik. Ezért az eddig alkalmazott próbák paraméteres próbák voltak (t-próbák, variancia analízis, a korreláció szignifikanciája, F-próba). A statisztikai módszerek egy fontos részénél nincs szükség az eloszlásra vonatkozó feltételekre. Ezeket a próbákat nemparaméteres próbáknak nevezzük.
A nemparaméteres módszereket általában tehát akkor alkalmazzuk, amikor a paraméteres próba nem alkalmazható. Ez akkor fordul elõ, ha a minta nem normális eloszlású populációból származik, vagy az eloszlás típusa nem ismert, és nem tudjuk, vagy nem akarjuk ellenõrizni (ismeretes, hogy a normalitás vizsgálat c 2 próbával kis elemszám esetén nem megbízható). Akkor is elõfordulhat, ha olyan típusú adatokkal dolgozunk, amelyekre nincs megfelelõ paraméteres próba, például ordinális típusú adatok esetén. (3 féle üdítõrõl meg tudjuk mondani, hogy melyiket szeretjük legjobban, melyiket legkevésbé, tehát fel tudunk állítani egy rangsort közöttük, de azt már nem tudjuk megmondani, hogy "mennyivel" szeretjük jobban az egyiket, mint a másikat.
Különbözõ kísérleti helyzetekre sokféle nemparaméteres próba létezik. Lényegében a legtöbb paraméteres próbához kidolgozták annak nemparaméteres megfelelõjét. Mi ezek közül csak 3 egyszerû esetet tanulunk.
Egy dolgot meg kell jegyeznünk. Általában, ha olyan adataink vannak, és olyan a hipotézisünk, amelyre létezik megfelelõ paraméteres próba, akkor azt alkalmazzuk inkább. A paraméteres próbáknak nagyobb az erejük, mivel figyelembe veszik az eloszlás bizonyos tulajdonságait (pl. az alakja normális), amelyet a nemparaméteres próbák nem vesznek figyelembe.
Gyakran felmerülõ kérdés: "mi történik, ha paraméteres próbát alkalmazok annak ellenére, hogy az adataim nem igazán felelnek meg a követelményeknek?" Jelenleg is folyik a kutatás erre a kérdésre vonatkozóan. Például, a t-próba alkalmazásakor feltesszük, hogy a populációk normális eloszlásúak. De a kutatás bebizonyította, hogy sokszor a t-próba eredménye elfogadható akkor is, ha a populációk eloszlása többé-kevésbé eltér a normális eloszlástól. A próbának az olyan tulajdonságát, amely akkor is mûködik, amikor az elméleti feltételek nem teljesülnek, robusztusságnak nevezzük.
Az adatok rangsorolása
A nemparaméteres próbák nem tudják használni a populáció-paraméterek becsléseit, helyette ragszámokat alkalmaznak. Az eredeti adatainkból csak azok nagyságrendi viszonyait veszik figyelembe. Ha két adat közül az egyik nagyobb, mint a másik, akkor csak ezt a tényt veszik figyelembe, és nem azt, hogy mennyivel nagyobb. Ehhez az adatokat rangsorolni kell. A nemparaméteres próbák az eredeti adatok helyett a megfelelõ rangszámokkal dolgoznak. A rangszámok képzését a következõ példán mutatjuk be. Tegyük fel, hogy a következõ mérési adataink vannak:
199, 126, 81, 68, 112, 112.
A negyedik elem (68) a legkisebb, õ kapja az 1-es rangszámot. A következõ legkisebb elem a 3-ik, az õ rangszáma 2. A nagyság szerinti sorrendben a következõ két elem egyenlõ, ezért az õ rangszámuk a következõ két rangszám, a 3 és 4 átlaga: 3,5. Az ilyen rangszámokat kapcsolt rangoknak nevezzük. Végül a 126, ill. 199 -es elem megfelelõ rangszáma 5, ill. 6. A rangsorolás eredményét a táblázat szemlélteti.
|
Esetszám |
Adat |
Rang |
|
1 |
199 |
6 |
|
2 |
126 |
5 |
|
3 |
81 |
2 |
|
4 |
68 |
1 |
|
5 |
112 |
3.5 |
|
6 |
112 |
3.5 |
Az összes rangszám összege az elsõ n egész szám összege, azaz 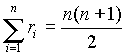 kell, hogy legyen. Ezzel ellenõrizhetjük a rangsorolásunk helyességét. Most a rangszámok összege 21, és 6ž
7/2=21.
kell, hogy legyen. Ezzel ellenõrizhetjük a rangsorolásunk helyességét. Most a rangszámok összege 21, és 6ž
7/2=21.
Egymintás próbák: az elõjelpróba és az elõjeles rangpróba
Az egymintás t-próbát összefüggõ adatok, önkontrollos kísérletek kiértékelésére alkalmazzuk, azt teszteljük, hogy a populációk átlagai ugyanazok. Normális eloszlás esetén ezt a paraméteres próbát alkalmazzuk. Ha a normalitást nem tudjuk feltételezni, vagy nem akarjuk ellenõrizni, nemparaméteres próbát kell alkalmaznunk.
Az elõjel-próba nemparaméteres próba, amely azt a nullhipotézist teszteli, hogy két összefüggõ minta ugyanabból a populációból származik. Elvégzésének nem feltétele a normalitás.
Az elõjelpróba elvégzéséhez elõször képezzük a két minta különbségét, majd megszámoljuk a negatív és a pozitív különbségek számát. Ha az eredeti két változó azonos eloszlású, akkor körülbelül azonos számú negatív és pozitív különbséget kapunk.
A próbához kis mintaelemszám esetére van egy táblázat, amelyben megtalálható, hogy adott mintaelemszám esetén hány különbség tekinthetõ szignifikánsnak. Nagy mintaelemszám esetén (>30), adható egy olyan formula, amelyre már a normális eloszlás táblázata használható a p-érték megkeresésére.
Az elõjeles rangpróba (egymintás Wilcoxon-próba) nemcsak az elõjeleket, hanem a különbségek közötti nagyságrendeket is figyelembe veszi, így nagyobb erejû, mint az elõjelpróba. Végrehajtása a következõ: a mintaelemek közötti különbségeket rangsoroljuk az elõjelektõl függetlenül, majd összeadjuk a pozitív különbségekhez tartozó rangszámokat (vagy a negatív különbségekhez tartozó rangszámokat, tetszés szerint, elég az egyiket). Az egyik rangszám-összeg alapján lehet dönteni egy táblázat segítségével. A táblázat a mintaelemszámhoz tartozó Rmin-Rmax értékeket tartalmazza. Ha valamelyik rangszámösszeg beleesik az intervallumba, akkor megtartjuk a nullhipotézist, a két minta ugyanolyan eloszlású populációból származik, ha a rangszámösszegek az intervallumon kívül esnek, akkor szignifikáns különbség van közöttük, a nullhipotézist elvetjük.( Az intervallumok a táblázatban úgy vannak megadva, hogy ha az egyik ragszámösszeg beleesik, akkor a másik is és fordítva).
Példa. 13 tanuló olvasási sebességét vizsgálták meg egy tanfolyam kezdetekor és a végén. Tegyük fel, hogy az olvasási sebességet mérõ számok eloszlása nem normális, tehát az egymintás t-próba nem alkalmazható. Az elõjeles rangpróbát végezzük el helyette a következõképpen:
H0: a két minta ugyanazon populációból származik.
A pozitív rangok összege R+=40.5, a negatívoké R-=25.5. 95%-os szinten a táblabeli intervallum 10-56. Mivel mindkét rangszámösszeg beleesik az intervallumba, nem vetjük el a nullhipotézist, nem mutatható ki szignifikáns különbség az olvasási sebesség változásában 95 %-os szinten
|
Tanuló |
Értékelés a tanfolyam kezdetén |
Értékelés a tanfolyam végén |
Különbség |
Rang |
|
1 |
50 |
52 |
-2 |
5.5 |
|
2 |
48 |
51 |
-3 |
9 |
|
3 |
46 |
46 |
0 |
|
|
4 |
50 |
49 |
1 |
2 |
|
5 |
62 |
50 |
2 |
5.5 |
|
6 |
80 |
70 |
10 |
11 |
|
7 |
23 |
21 |
2 |
5.5 |
|
8 |
30 |
33 |
-3 |
9 |
|
9 |
45 |
46 |
-1 |
2 |
|
10 |
53 |
53 |
0 |
|
|
11 |
49 |
48 |
1 |
2 |
|
12 |
51 |
48 |
3 |
9 |
|
13 |
46 |
48 |
-2 |
5.5 |
Nagy mintaelemszám esetére egy közelítõen normális eloszlású statisztika segítségével a normális eloszlás alapján vizsgálható a szignifikancia. A számítógépes programrendszerek általában csak ezt a normális közelítésbõl származó p-értéket számítják ki még kis mintaelemszám esetén is, amikor pedig a közelítés nem túl jó. Számítógép használata esetén tehát kis mintaelemszámnál érdemes a táblázatból ellenõrizni a szignifikanciát.
Kétmintás próba: a Mann-Whitney U próba vagy kétmintás Wilcoxon próba
A Mann-Whitney próba, amelyet egyes könyvek Wilcoxon féle kétmintás próbának hívnak, két független mintára vonatkozó hipotézist tesztel. A kétmintás t-próba nemparamétres megfelelõje. Nem feltétele a normalitás, és alkalmazható nemcsak intervallum, hanem ordinális változókra is.
A nullhipotézis: a minták ugyanazon populációból származnak.
A próba végrehajtása: a két mintát együtt rangsoroljuk (azaz, megállapítjuk az egyesített minta rangszámait). Majd összeadjuk külön az egyik és külön a másik minta rangszámait. Ha igaz a nullhipotézis, hogy a minták ugyanazon populációból származnak, akkor e két rangszámösszeg közel egyenlõ kell, hogy legyen. Minél jobban eltér az egyik összeg a másiktól, annál több okunk van feltételezni, hogy a két minta különbözõ eloszlású populációkból származik. A döntéshez kis elemszám esetén táblázat áll rendelkezésre, nagy elemszám esetén normális eloszlásra történõ közelítõ formula van. A számítógépes programok az egymintás esethez hasonlóan ez utóbbit számítják ki, így kis elemszám esetén érdemes a táblázatot is megnézni. A táblázat általában egy intervallumot tartalmaz, amelybe ha beleesik valamelyik rangszámösszeg, akkor nem szignifikáns a különbség, ha kívül esik, akkor elvetjük a nullhipotézist.
Példa.
King (1992) patkányokban vizsgálta a diéta és a tumornövekedés közötti kapcsolatot. Az állatok egyik csoportja telített, a másik telítetlen zsírokat tartalmazó diétát kapott. A vizsgálat egyik hipotézise az volt, hogy tumor kifejlõdési ideje különbözik-e a két csoportban. Ha feltételezzük a normális eloszlást, kétmintás t-próbával vizsgálhatnánk azt a nullhipotézist, hogy a két populáció-átlag ugyanaz. Mivel az idõk eloszlása nem tûnik normálisnak, és ráadásul a mintaelemszám is kicsi ahhoz, hogy a normalitást ellenõrizzük, olyan statisztikai próbát kell alkalmaznunk, amelynek nem feltétele a normalitás. A következõ táblázat foglalja össze a kísérlet adatait
|
Telített |
Telítetlen |
||||
|
Esetszám |
Idõ |
Rang |
Esetszám |
Idõ |
Rang |
|
1 |
199 |
9 |
4 |
68 |
3 |
|
2 |
126 |
8 |
5 |
112 |
6.5 |
|
3 |
81 |
5 |
6 |
112 |
6.5 |
|
4 |
50 |
1 |
4 |
80 |
4 |
|
5 |
51 |
2 |
|||
|
Összeg |
25 |
20 |
Az elsõ csoport rangszámösszege, R
1=25, a másodiké R2=20.Ha az elemszám kicsi, a táblázatbeli értékekkel kell összehasonlítanunk e rangszámösszegeket. Esetünkben az 5-4 elemszámokhoz tartozó intervallum (10-26), mindkettõt tartalmazza, a különbség nem szignifikáns.
A rangkorreláció
A Pearson féle korrelációs együtható csak olyan adatokra alkalmazható, amelyeket legalábbis intervallum skálán mértek. Ha még hipotézis vizsgálatot is szeretnénk végezni a korrelációs együtthatóra, akkor a normalitást is fel kell tennünk. Az olyan adatokra, amelyek vagy nem normális eloszlásúak, vagy nem intervallum skálán mérték, egy másik mérõszám, az ún. Spearman féle rangkorrelációs együttható áll rendelkezésre.
A rangkorrelációs együttható a rangszámok közötti Pearson korrelációs együttható, ha nincsenek kapcsolt rangok. Az így kiszámított korrelációs együttható tehát szintén -1 és +1 között veszi fel értékeit, és az értelmezése is ugyanaz, kivéve, hogy itt most rangszámokat, nem az eredeti értékeket hasonlítjuk össze.
Létezik egy rövidebb formula a rangkorrelációs együttható kiszámítására:
|
Az 1. minta rangszámai |
A 2. minta rangszámai |
A rangszámok különbsége |
|
r 1 |
q 1 |
d 1=r1-q1 |
|
r 2 |
q 2 |
d 2=r2-q2 |
|
... |
... |
... |
|
r n |
q n |
d n=rn-qn |
Ha d
i jelöli két rangszám különbségét, akkor a rangkorrelációs együttható a következõ formulával számítható ki: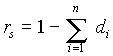
A Pearson féle korrelációs együtthatóhoz hasonlóan a rangkorrelációra is végezhetünk szignifikancia vizsgálatot. Ha azt a nullhipotézist szeretnénk tesztelni, hogy a rangkorrelációs együttható a populációban = 0, akkor ugyanaz a formula alkalmazható, mint a Pearson f. korrelációs. együttható esetében, azaz
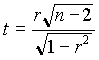 t-eloszlást követ n-2 szabadságfokkal.
t-eloszlást követ n-2 szabadságfokkal.