
A Gauss haranggörbe szemmel látható
an elég jól illeszthető!Gauss papíron ábrázolva az empirikus eloszlásfüggvényt közel egyenest kapunk!
Sz13Mi 2. beszámoló 2001.12.12 1.csoport
Név:
Neptun kód:
Szül.idő
:A H:hálózati meghajtó SPSS könyvtárában található ez a WORD dokumentum, ezt kell kitöltenie!
1. Másolja a G:\KOZOS\SZ13MI\ZH2\varosok.sav fájlt az írható D: meghajtóra!
2. Indítsa el reá az SPSS-t!
3. Az Edit/options/general menüben állítsa át az spss.jnl journal fájl helyét
Record syntax editor és Append módban a H\SPSS könyvtárra!
4. Display labels. paranccsal listázza ki a változók cimkéit (az oszlopnevek jelentését).
List of variables on the working file
|
Name |
Position |
Label |
|
TELKOD |
1 |
Településkód |
|
TELNEV |
2 |
Településnév |
|
TERULET |
6 |
Település területe (hektár) |
|
POPU |
7 |
Állandó népesség száma (fő) |
|
OREGINDX |
8 |
Öregségi mutató (ha x>1) |
|
VANDKUL |
9 |
Vándorlási különbözet (x>1=kivándorlás) |
|
SZEMAUTO |
10 |
Az 1000 lakosra jutó személygépkocsik száma (db) |
|
MVALLALK |
11 |
Az 1000 lakosra jutó működő vállalk ozások száma |
|
EVALLALK |
12 |
Az ezer lakosra jutó egyéni vállalkozások száma |
|
MUNKNELK |
13 |
A regisztrált munkanélküliek aránya a 18-59 évesekre vetítve |
|
TARTOSMN |
14 |
A tartósan munkanélküliek aránya 18-59 évesek között |
|
LAKASOK |
15 |
Az egy lakásra jutó állandó lakosok száma (db) |
|
TAVBVONA |
16 |
Az 1000 lakosra jutó távbeszélő fővonalak száma |
|
UZLTELEF |
17 |
A egy működő vállalkozásra jutó telefonvonalak száma |
|
TELARANY |
18 |
Az üzleti fővonalka aránya az összes fővonalon belül |
|
NETSZOLG |
19 |
Az internetes szolgáltatási formák száma (teljes skála=10) |
|
INT_SZOL |
20 |
Internet szolgáltatók száma |
|
INF_KEPK |
21 |
Középfokú informatikai képzést biztosító iskolák száma |
|
KOZFOKIN |
22 |
Az összes középfokú intézmény száma |
|
INF_KEPF |
23 |
Informatikus képzés a felsőoktatásban (Iskolaszáma) |
|
FELDIP |
24 |
IKT feldolgozó ipari cégek száma |
|
TERMSZOL |
25 |
IKT termékhez kapcsolódó szolgáltatást nyújtó cégek száma |
|
NOTERMSZ |
26 |
Termékhez nem kapcsolódó IKT szolgáltatást nyújtó cégek száma |
|
IKT_ALL |
27 |
Az összes IKT cég száma |
|
MEDGAZD |
28 |
A média gazdaságban érintett cégek száma |
|
CEG_ALL |
29 |
Az összes gazdasági szervezet száma |
|
JOVED99 |
30 |
Az egy főre jutó személyi jövedelemadó alap (Ft) |
|
SZJA99 |
31 |
Az egy főre jutó befizetett SZJA (Ft) |
|
IKT_MEDG |
32 |
Az IKT szektorban és a médiagazdaságban érdekelt cégek száma |
|
ELVSZUL |
33 |
Élveszületések száma (fő) |
|
HALALOZ |
34 |
Halálozások száma (fő) |
|
ORVOS |
35 |
Dolgozó orvosok száma |
|
TERALTIS |
36 |
Általános iskolai termek száma |
|
TERKOZIS |
37 |
Középiskolai termek száma |
|
LAKALLOM |
38 |
Lakásállomány |
|
NAGYLAK |
39 |
Az év folyamán épített 4 szobás vagy nagyobb lakások száma |
5. Ellenőrizze, hogy az 1000 főre jutó személygépkocsik száma normális eloszlásúnak tekinthető-e?
a/ jól illesztett normális eloszlású görbével kiegészített hisztogramot kérjen reá! (3 pont)
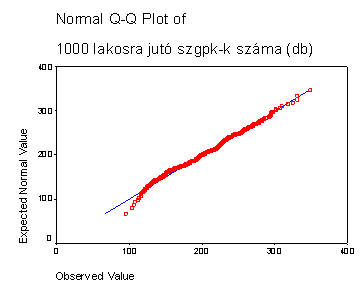
b/ Q-Q plot-ot kérjen reá! (3 pont)
c/ Az egy mintás Kolmogorov-Szmirnov tesztet normalitásvizsgálatra használja (5 pont)
Válaszok:
|
|
|
|
A Gauss haranggörbe szemmel látható an elég jól illeszthető! |
Gauss papíron ábrázolva az empirikus eloszlásfüggvényt közel egyenest kapunk! |
|
|
Mivel a szignifikancia szint 0.492 és ez meghaladja a 0,05-öt, ezért az eloszlást normális eloszlásnak tekinthetjük . |
6. Hozzon létre egy “meret” nevű ordinális változót melybe 1 kerül, ha az állandó népesség száma kisebb mint 30000, és 2 kerül, ha az állandó népesség száma legalább 30000. (5 pont)
A generált parancsok:
RECODE
popu
(Lowest thru 29999=1) (30000 thru Highest=2) INTO meret .
EXECUTE .
FORMATS meret (F1).
VARIABLE LABELS meret "Városméret".
VALUE LABELS meret
1.00000000000000 "kisváros"
2.00000000000000 "nagyváros"
.
Az előző csoportonkénti (kisváros, nagyváros) leíró statisztikát kérje ki az 1000 főre jutó személygépkocsik számára! (10 pont)
(plot-ok nem kellenek!)
Válaszok:

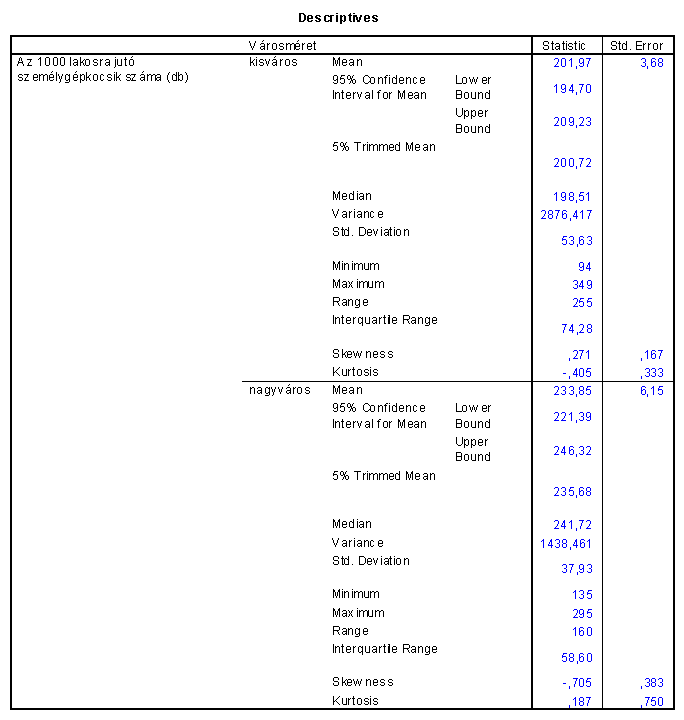
1. csoport átlag:
szórás:
konfidencia intervallum:
2. csoport átlag:
szórás:
konfidencia intervallum:
( A fenti táblázat tartalmazza ezen értékeket is!)Látható, hogy a nagyvárosokban az ezer főre jutó személygépkocsik száma jelentősen nagyobb!
7. Két faktort kérve végezzen fak
toranalízist (főkomponens) a demográfiai adatok felhasználásával! (14 pont)A faktortérbeli koordinátákat x1 x2 néven mentse el!
Eredmények:
A generált (és javított) parancs:
FACTOR
/VARIABLES popu elvszul halaloz vandkul oregindx
/MISSING LISTWISE
/ANALYSIS popu elvszul halaloz vandkul oregindx
/PRINT INITIAL CORRELATION DET KMO REPR EXTRACTION ROTATION
/FORMAT BLANK(.10)
/PLOT ROTATION
/CRITERIA FACTORS(2) ITERATE(25)
/EXTRACTION PC
/CRITERIA ITERATE(25)
/ROTATION VARIMAX
/SAVE REG(ALL x)
/METHOD=CORRELATION .
KMO mérték:
Bartlett teszt:

Mivel a KMO mérték > 0.5, ezért a feladat alkalmas faktoranalízisre.
A Bartlett próba H0 hipotézise (a változók függetlenek) a szignifikancia szint <0.05 miatt elvetendő, tehát a változóink összefüggnek, így van értelme a faktoranalízisnek.
Sajátértékek:
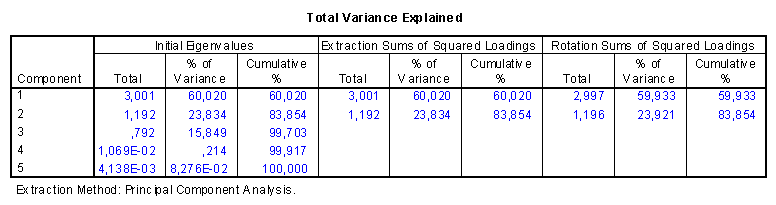
Látható, hogy az el
ső két faktor sajátértéke(eigenvalues) nagyobb 1-nél, és ezek együtt az eredeti adatainkat jól reprezentálják (83.854 %)
Rotált faktormátrix:
Faktorok jelentése:
|
|
Az első faktor additív adatokkal (népességszám, élveszületések száma, halálozások száma) van kapcsolatban, így ezt méret faktornak nevezhetjükA második faktor relatív adatokkal a vándorlási különbözettel és az öregségi index-szel (fordítva)van kapcsolatban. Ez azt jelenti, hogy amikor az odavándorlás több, mint az elvándorlás, akkor általában a fiatalok száma növekszik és ez az öregségi indexre is kihat. Éppen ezért ezt dinamizmus faktornak nevezhetjük. |
8. Kérjen szimpla felhődiagramot a két faktorváltozóra!
A diagramon a leginkább kiló
gó két pontra tegye reá a Point ID-t és az ide másolt grafikus objektumban ezeket az azonosító kódokat cserélje le a települések nevére! (legegyszerűbb, ha a scatterplot ID a településnév) (10 pont)Scatterplot:
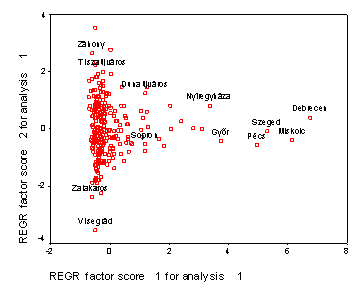
Látható, hogy jobbra a nagy városok, fent a dinamikusabbak, lent pedig a több idősebb lakossal rendelkező úgynevezett pihenővárosok vannak.
9. A településeket ossza legalább 5 csoportba K-mean klaszterezéssel! A csoportok kezdőpontjait a felhődiagram alapján adja meg! A csoporttagsági kódokat “csoport”, a csoportközéppontoktól mért távolságokat “tavolsag” új változókba mentse el! (15 pont)
Válaszok
:A scatterplot alapján Szeged, Dunaújváros, Tatabánya, Zalakaros, Tiszaújváros megfe
lelő kezdőcentrum lehet, így a koordinátáikat felhasználhatjuk a kezdőpontok megadásához.A generált (és módosított) parancs:
QUICK CLUSTER
x1 x2
/MISSING=LISTWISE
/CRITERIA= CLUSTER(5) MXITER(30) CONVERGE(0)
/METHOD=KMEANS(NOUPDATE)
/SAVE CLUSTER(csoport) DISTANCE(tavolsag)
/INITIAL=(1.2,1.2 0.6,-2.4 -0.3,2 2,0 5.3,0)
/PRINT INITIAL.
A/ csoportok elemszáma:

B/ csoportközéppontok végső koordinátái:
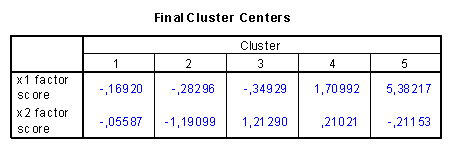
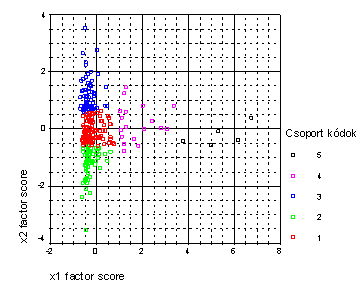
Az osztályozás utáni scatterplot
:
10. Mentse el a táblázatát excel formában, amiből törölje ki a
telnev,x1,x2,csoport,tavolsag oszlopokon kívül minden egyéb oszlopot! Rendezze le az adatokat csoport, majd ezen belül tavolsag szerint növekvőleg, majd csak a csoportok első elemét hagyja meg, a többit törölje ki. Így a csoportok legtipikusabb egyedeit kapja meg.(5 pont)
Csoportok legtipikusabb városai (telnev,x1,x2,csoport,tavolsag):
|
TELNEV |
X1 |
X2 |
CSOPORT |
TAVOLSAG |
|
Sárvár |
-0,223 |
-0,028 |
1 |
0,061 |
|
Mezőberény |
-0,276 |
-1,184 |
2 |
0,010 |
|
Lenti |
-0,430 |
1,169 |
3 |
0,092 |
|
Tatabánya |
2,044 |
-0,012 |
4 |
0,401 |
|
Szeged |
5,295 |
-0,078 |
5 |
0,159 |