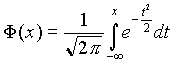
A matematikai statisztika egyike a matematika azon ágainak, amelyet a gyakorlatban nagyon sok területen alkalmaznak. Használják a műszaki tudományokban, a minőségellenőrzésben, az orvostudományban, a közgazdaság tudományban és még számos helyen. Elterjedésének oka kettős: Egyrészt a világ jelenségei igen gyakran nem determinisztikusak, hanem sztochasztikusok, másrészt gyakran nem ismerjük az egész sokaságot, csak mintát veszünk belőle. A minta paraméterei alapján adunk becslést az egész sokaság megfelelő paramétereire. A biológia, orvostudományban végzett mintavételek kiértékelését biostatisztikának nevezzük. Az egyetemen egyre szélesebb körben sajátítják el a diákok a biostatisztika alapjait. Ezen tanulmányok megértését próbáljuk segíteni e gyakorlati példatárral. A példatár elméleti ismereteket nem tartalmaz. Néhány hasznos irodalmat azonban megadunk, az érdeklődők itt alapos ismereteket szerezhetnek a problémák elméleti hátteréről.
A példatár felépítése a IV. éves gyógyszerész hallgatók tananyagát követi. Minden esetben megadunk legalább egy kidolgozott minta példát, majd néhány a feladattípushoz kapcsolódó példát. A példatár végén vegyesen 40 példa található, melyek megoldása a témakörönként rendezett feladatok alapján könnyen megoldható.
Eredményes, jó munkát kívánunk a példatár használatához!
A Szerzők
1. Eloszlás, eloszlásfüggvény
1. Legyen a kísérlet 3 pénz egyidejű feldobása. Legyen a valószínűségi változó a következő: X=fej dobások száma. Készítsük el ennek a változónak az eloszlását és eloszlásfüggvényét:
Elemei események: III, IIF, IFI, IFF, FII, FIF,FFI, FFF (összes lehetséges eset: 8)
|
Fejdobások száma (X) |
0 |
1 |
2 |
3 |
|
P(X) |
|
|
1. |
1. |
|||||||||||||||||||||
|
|
0.5 |
0.5 |
|||||||||||||||||||||
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
||||||||||||||||
Eloszlás Eloszlásfüggvény : F(x)=P(X<x)
Megoldás:
|
Fejdobások száma (X) |
0 |
1 |
2 |
3 |
|
P(X) |
1/8 |
3/8 |
3/8 |
1/8 |
Elemei események:
Fejdobások száma 0: 1 darab (III); (összes lehetséges eset: 8)
Fejdobások száma 1: 3 darab (IIF, IFI, FII);
Fejdobások száma 2: 3 darab (IFF, FIF,FFI,);
Fejdobások száma 3: 1 darab (FFF);
|
1. |
1. |
||||||||||||||||||||||
|
0.5 |
0.5 |
||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
1 |
2 |
3 |
4 |
||||||||||||||||
Eloszlás Eloszlásfüggvény : F(x)=P(X<x)
2. A következő eloszlásokról állapítsuk meg, hogy valószínűségi eloszlások-e:
|
X |
0 |
5 |
10 |
15 |
20 |
|
P(X) |
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
Eloszlásfüggvény
|
X |
0 |
2 |
4 |
6 |
|
P(X) |
1/4 |
1/8 |
1/16 |
9/16 |
Eloszlásfüggvény
|
X |
0 |
2 |
4 |
6 |
|
P(X) |
-1 |
1.5 |
0.30 |
0.2 |
Nem eloszlásfüggvény
|
X |
0 |
2 |
4 |
6 |
|
P(X) |
1/4 |
1/8 |
1/16 |
2/16 |
Nem eloszlásfüggvény
Normális eloszlás
|
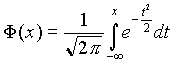
x |
F (x): x-től balra eső terület |
|
-4 |
0.0003 |
|
-3 |
0.0013 |
|
-2.58 |
0.0049 |
|
-2.33 |
0.0099 |
|
-2 |
0.0228 |
|
-1.96 |
0.0250 |
|
-1.65 |
0.0495 |
|
-1 |
0.1587 |
|
0 |
0.5 |
|
1 |
0.8413 |
|
1.65 |
0.9505 |
|
1.96 |
0.975 |
|
2 |
0.9772 |
|
2.33 |
0.9901 |
|
2.58 |
0.9951 |
|
3 |
0.9987 |
|
4 |
0.99997 |
Egy városi kórházban az újszülöttek testsúlyai normális eloszlásúak N(3500,400) paraméterekkel. Legyen X egy véletlenszerűen kiválasztott újszülött súlya.:
a) Mi a valószínűsége, hogy egy újszülött súlya 3500 alá esik?
b) Adjuk meg azt az intervallumot, amelybe várhatóan az adatok középső 95%-a esik!
Megoldás:
a) Mi a valószínűsége, hogy egy újszülött súlya 3500 alá esik?
P(x <3500)=F ((3500-3500)/400)= F (0)=0.5
b) Adjuk meg azt az intervallumot, amelybe várhatóan az adatok középső 95%-a esik!
P(x1<x <x2)=F ((x2-3500)/400)- F ((3500- x1)/400)= 0.95=2F (x)-1
Innen x=784;x1=2716;x2=4284
Konfidencia intervallum, t-ptóba, szignifikancia
Egy kezelés során szükségessé vált annak ellenőrzése, hogy az milyen hatással van a vérnyomásra. A vizsgált paciensek korcsoportjában a systolés vérnyomás normálértéke 165. n=9 személyt megmérve a következő érté
keket kapták:182.00 152.00 178.00 157.00 194.00 163.00 144.00 114.00 174.00
Az átlag=162 Hgmm volt, a standard deviáció SD=23.92 lett.
a) Számítsuk ki a standard errort.
SE=.SD/Ö n= 7.973333333333.
b) Adjuk meg a populáció-átlagra vonatkozó 95%-os konfidencia intervallumot! (t8, 0.05=2.306)
(átlag - t*SE, átlag + t * SE )= 162-2,306* 7.973= 143.613493; 162+2,306* 7.973= 180.386507
Mit ad meg ez az intervallum?
.......................................................................................................................................................
.......................................................................................................................................................
.......................................................................................................................................................
c) Mondhatjuk-e a konfidencia intervallum alapján 95% biztonsággal, hogy a minta-adatok 165 átlagú populációból származnak?
Igen ---- Nem
Indokoljuk a döntést
d) Válaszoljunk az előbbi kérdésre úgy, hogy számítsuk ki a próbastatisztikát:
t= (átlag - 165)/SE=-3/7.973=- 0.3762699109495.......
és hasonlítsuk a t8, 0.05=2.306 táblázatbeli értékhez.
Van-e szignifikáns különbség a mintaátlag és a populációátlag között 95 %-os szinten? Nincs
Miért?
Nincs, mert a számított p érték kisebb, mint a táblázatbeli.
e) SPSS program által adott p-érték=0.717 Válaszoljunk az előbbi kérdésre a p-érték alapján.
Nem szignifikáns a különbség, mert p>0.05
.......................................................................................................................................................
Kétmintás t-próba
1. Egy felmérés során szegedi és debreceni középiskolás tanulólányok testsúlyairól a következő adatokat kapták:
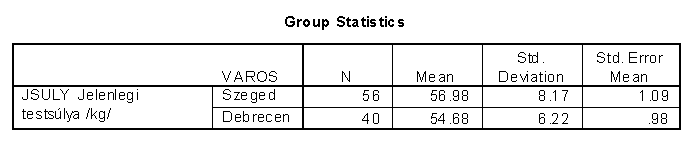
A testsúly átlagokat kétmintás t-próbával hasonlították össze.
Mi a nullhipotézis?...A szegedi és debreceni diákok testsúlya megegyezik!
A t-próba t-értéke t=1.502.
Mennyi a szabadságfok? (n1+n2-2)=94
A p-érték p=0.136
Van-e szignifikáns különbség a két populáció átlaga között 95%-os szinten?..nincs
Miért?. p>0.05
2. Egy másik, hasonló felmérés szerint (melyben szintén középiskolás tanulólányokat kérdeztek, de másik, reprezentatív mintát), a következő eredményeket kapták:
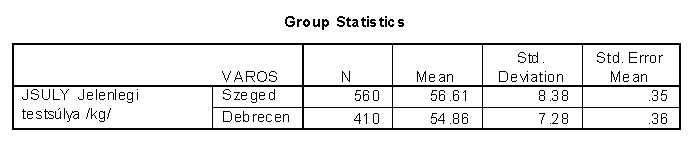
A t-próba t-értéke most t=3.4.
Mennyi most a szabadságfok? 968
A p-érték p=0.001
Van-e szignifikáns különbség a két populáció átlaga között 95%-os szinten? Igen
Miért?...........................................................................................................................................
A számított p érték nagyobb, mint a táblázatbeli.
Mindkét esetben kb. ugyanannyi volt at átlagok közötti különbség.
Lát-e ellentmondást a két kísérletből levont következtetések között, és mivel tudná indokolni?
Az elemszámokból adódóan a 2. példában lényegesen kisebb a Std. Error érték.
Kétmintás t-próba feladat megoldása
1. Egy felmérés során szegedi és debreceni középiskolás tanulólányok testsúlyairól a következő adatokat kapták:
A testsúly átlagokat kétmintás t-próbával hasonlították össze.
Mi a nullhipotézis?..A debreceni és szegedi populációban azonos a lányok testsúly-átlaga (m Debrecen=m Szeged. )..............................................................
A t-próba t-értéke t=1.502.
Mennyi a szabadságfok? ..56+40-2=94.........................
A p-érték p=0.136
Van-e szignifikáns különbség a két populáció átlaga között 95%-os szinten?..nincs.................
Miért?.0.136 > 0.05......................................................................................................................
2. Egy másik, hasonló felmérés szerint (melyben szintén középiskolás tanulólányokat kérdeztek, de másik, reprezentatív mintát), a következő eredményeket kapták:
A t-próba t-értéke most t=3.4.
Mennyi most a szabadságfok? .560+410-2=968.........................
A p-érték p=0.001
Van-e szignifikáns különbség a két populáció átlaga között 95%-os szinten?.igen....................
Miért?..0.001 < 0.05.................................................................................................................
Mindkét esetben kb. ugyanannyi volt az átlagok közötti különbség.
Lát-e ellentmondást a két kísérletből levont következtetések között, és mivel tudná indokolni?
A döntés különböző a két esetben, az átlagok közötti különbség és a szórás kb. ugyanaz. A t-érték annál nagyobb,(ennek megfelelően a p-érték annál kisebb), minél nagyobb az átlagok közötti különbség, minél kisebb a szórás és minél nagyobb az elemszám.
Azt nem tudjuk, hogy a populáció-átlagok azonosak-e. De az első esetben mivel azt döntöttük, hogy nincs különbség, a második fajta hibát követhettük el, aminek a hibavalószínűsége kis elemszám esetén elég nagy lehet. A p-érték kicsi, de nem szignifikáns. Így az első esetben csak azt tudjuk mondani, hogy a különbség k
imutatásához nincs elegendő információ az adatok alapján, 5% döntési hibát megengedve. 15% döntési hibát megengedve, a különbséget szignifikánsnak mondhatnánk, ám 15% túl nagy hiba.A második esetben a döntésünk alapján azt mondjuk, hogy a két populáció átlaga különböző. Ha hibásan döntöttünk, akkor az első fajtát követhettük el, amelynek valószínűsége <0.05. Ha valójában nincs különbség a populációk között, akkor annak valószínűsége, hogy ekkora (2 kg), vagy még nagyobb eltérést kapjunk, 0.001, tehát nagyon kicsi.
Röviden: nagy elemszám esetén kis különbségek is szignifikánssá válnak, míg kis elemszám esetén nagy különbségek is lehetnek nem szignifikánsak.
Korreláció
Egy élelmiszeripari csoport 3369 embert kérdezett meg, mennyinek gondolják bizonyos általánosan ismert ételek kalóriaértékét. A következő táblázat mutatja az egyes ételek megsejtett kalóriaértékeinek átlagát, és a valódi kalóriaértékeket.
|
Étel |
Sejtett kalória |
Korrekt kalória |
|
1 adag sajtos makaróni |
350 |
270 |
|
Egy szelet fehér kenyér |
120 |
60 |
|
Egy pohár tej |
200 |
160 |
|
Közepes méretű alma |
110 |
80 |
|
Közepes méretű krumpli |
160 |
88 |
2. Milyennek látja az összefüggést az ábra alapján?
Pozitív vagy negatív az összefüggés iránya?.............................................
Hozzávetőleg lineáris az összefüggés?..............................................
Vannak-e kilógó értékek (outliers)?..................................................................................
3. A korrelációs együttható értéke r=0.981.
Határozzuk meg a korreláció t-értékét: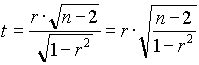 
.........................
Számítsuk ki a szabadságfokot:..................................
A táblázatbeli t-érték t3,0.05=3.182
Hasonlítsuk össze a mi általunk számított t-érték abszolút értékét a táblabelivel.
Szignifikáns-e a korreláció 95% -os szinten?.......................................
4. Az SPSS program által adott p-érték p=0.003. Ennek alapján ellenőrizzük az előbbi döntésünket a
korrelációs együttható szignifikanciájáról. Ugyanaz?……………A számítások alapján ismét magyarázzuk meg a sejtett és a korrekt kalóriaértékek közötti összefüggést.
A vizsgán kézi számolással megoldandó feladattípusok
Adattípusok
1. Milyen adattípusok vannak aszerint, hogy milyen tulajdonságot képviselnek?........................
Mi a különbség a nominális és ordinális változók között? ........................................................
Mondjon példát nominális változóra ..........................................................................
Mondjon példát ordinális változóra ...................................................................
Mondjon példát bináris (dichotóm) változóra ........................................................................
2. A következő feljegyzés egy eset orvosi jelentésének része
"A paciens 32 éves gazdálkodó, feleségével és 2 gyermekével együtt Kiskundorozsmán lakik. A fő panasza lázas állapot az utóbbi 3 hónapban. A fehérvérsejtszáma 8700 és az urin analízis eredménye normál."
Képezzen változókat a következő szempontok szerint!
A változó neve Adattípusa A paciensre vonatkozó értéke
...................... .................. .....................................
...................... .................. .....................................
...................... .................. .....................................
...................... .................. .....................................
...................... .................. .....................................
...................... .................. .....................................
...................... .................. .....................................
...................... .................. .....................................
Valószínűség
1. Egy kockát feldobva 6 lehetséges kimenetel van, Ha X jelöli a dobás eredményét, számítsuk ki a következő valószínűségeket: a) P(X=1); b) P(X>1); c) P(1<X<4)
2. Egy pénzérmét kétszer egymás után feldobunk. Soroljuk fel az elemi eseményeket! Mi annak a valószínűsége, hogy mindkét dobás írás?
3. Egy pénzt és egy kockát feldobunk. A lehetséges kimenetelek a következők: F1,F2,F3,F4,F5,F6,I1,I2,I3,I4,I5,I6. Számítsuk ki a következő események valószínűségét:
a) fej és páros dobás a kockával
b) fej vagy páros dobás a kockával
c) fej és 5-ös dobás
d) fej vagy 5-ös dobás
e) 4-es vagy 6-os dobás.
4. Jelölje x a glukóz súlyát 100 ml vérplazmában. Legyen x1 és x2 két rögzített érték (x1<x2). Legyenek A,B,C,D a következő események:
A: x<x1, B: x>x1, C: x<x2, D: x>x2.
Mely események zárják ki egymást?
5. 15 egeret megmérve a következő súlyokat kapták:
28 31 26 26 29 31 30 27 25 30 28 28 23 32 30
Mi a következő események relatív gyakorisága:
E: x<26, F: x=31, G: 26<x<31?
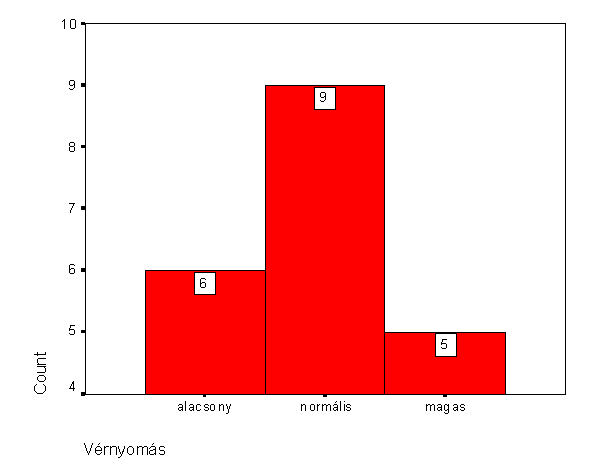
1. 20 ember vérnyomását mérték és csak azt figyelték, hogy a vérnyomás alacsony (A), normál (N), vagy magas (M) tartományba esik-e. A következő mintát kapták:
M,M,N,A,M,N,A,A,N,N,N,N,A,M,N,N,A,M,A,N
Készítsünk relatív gyakorisági hisztogramot a mintából, és interpretáljuk az eredményt.
2. Számítsuk ki a következő minták átlagát, standard deviációját, mediánját és terjedelmét. Ahol szükséges, alkalmazzunk transzformációt.
a) -2, 0, 2, 4, 6 (n=5)
b) 2, 5, 4, 2 (n=4)
c) 3, 5, 1, 0, 3, 4 (n=6)
d) 1002, 1005, 1004, 1002 (n=4).
3. Számolás nélkül hasonlítsuk össze a következő hőmérsékletek átlagát és standard deviációját:
Kodiak, Alaska: 10, 8, 0, -1
Coldfoot, Alaska: -10, -8, 0, 1
4. Számolás nélkül hasonlítsuk össze a következő életkorok átlag
át és standard deviációját:X: 5,2,7,3
Y: 65, 62, 67, 63
5. Adjunk meg egy ötelemű mintát, melynek a varianciája 0 .
1. Számítsuk ki a standard errort, ha a minta elemszáma n=16 és a standard deviáció sd=5.6.
Konfidencia intervallum, t-próbák
1. Számítsuk ki a standard errort, ha a minta elemszáma n=16 és a standard deviáció sd=5.6.
Ha a minta átlaga 12, mit tudunk mondani az átlag megbízhatóságáról (a =0.05, ttabla=2.13) ?
2. Egy vizsgálatban 10 egészséges nő systolés vérnyomá
sát mérve, az átlagra 119-et, a standard deviációra 2.1-et kaptak.a) mennyi a standard error becslése?
b) számítsunk 95%-os konfidencia intervallumot a populáció átlagára (a =0.05, ttabla=2.26).
c) mennyi itt a szabadságfok?
3. Egy vérnyomáscsökkentő gyógyszer kipróbálásakor a következő adatokat kapták
Gyógyszer nélkül Gyógyszer után
140 120
120 110
150 140
140 150
140 140
A különbség átlaga 6, a különbség standard errorja SE=4.65. Hatásos-e a gyógyszer (van-e különbség a két csoport átlagában)? Végezzük el a számítást kézzel, a szignifikanciát állapítsuk meg táblázatból (a =0.05, ttabla=2.57)
4. Egy lázcsillapító gyógyszer kipróbálásakor a következő adatokat kapták
Gyógyszer után - Gyógyszer előtt (különbségek)
1
0.5
1.5
-0.5
1
Hatásos-e a gyógyszer (eltér-e a különbség-átlag 0-tól)? (Átlag=0.7, se=0.34). Végezzük el a számítást kézzel, a szignifikanciát állapítsuk meg táblázatból (a =0.05, ttabla=2.78).
5. Tegyük fel, hogy a vérnyomást két különböző csoportban mértük meg, az egyik csoportot nem kezeltük (kontroll csoport, magas vérnyomásosok), a másodikat pedig kezeltük (kezelt csoport). Szeretnénk bebizonyítani, hogy a kezelés hatásos. Felté
ve, hogy a minták normális eloszlású populációból származnak, milyen próba alkalmas a kérdés eldöntésére? ...................................Az SPSS rendszerrel a próba eredménye a következő.
Variable Number of Cases Mean SD SE of Mean
------------------------------------------------------------------
Control 8 162.5000 10.351 3.660
Treatment 10 128.0000 11.353 3.590
------------------------------------------------------------------
Mean Difference = 34.5000
Levene's Test for Equality of Variances: F= .008 P= .930
t-test for Equality of Means 95%
Variances t-value df 2-Tail Sig SE of Diff CI for Diff
------------------------------------------------------------------
Equal 6.66 16 .000 5.183 (23.513, 45.487)
Unequal 6.73 15.67 .000 5.127 (23.613, 45.387)
------------------------------------------------------------------
Mondhatjuk-e, hogy a kezelés hatásos? (a =0.05).
6. Egy felmérés során szegedi és debreceni középiskolás tanulólányok testsúlyairól a következő adatokat kapták:
A testsúly átlagokat kétmintás t-próbával hasonlították össze.
Mi a nullhipotézis?.......................................................................................................................
.....................................................................................................................................................
A t-próba t-értéke t=1.502.
Mennyi a szabadságfok? ...............................
A p-érték p=0.136
Van-e szignifikáns különbség a két populáció átlaga között 95%-os szinten?............................
Miért?...........................................................................................................................................
Korreláció
n=5 megfigyelés (adatpár) alapján a korrelációs együttható értéke r=0.7.
Határozzuk meg a korreláció t-értékét: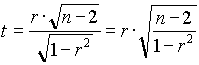 
.........................
Számítsuk ki a szabadságfokot:..................................
A táblázatbeli t-érték t3,0.05=3.182
Hasonlítsuk össze a mi általunk számított t-érték abszolút értékét a táblabelivel.
Szignifikáns-e a korreláció 95% -os szinten?.......................................
Chi-négyzet próbák
1. Harminc egyetemista lány között 10, ugyanennyi fiú között csak fele ennyi aktív sportolót találtak. Mondhatjuk-e ennek alapján, hogy a lányok közt magasabb a sportolók aránya? (95%-os szinten. (alfa=0.05, c 2tabla=3.84)) Mi itt a nullhipotézis?
2. Boldogít-e a pénz? ? 20 magas és 40 alacsony jövedelműt vizsgáltak meg, hogy elégedettek-e. A vizsgálat a magas jövedelműek felét, az alacsony jövedelműek 3/4-ét mutatta kiegyensúlyozottnak. Állapítsuk meg a megfelelő próbával, hogy van-e különbség a két csoport között 95%-os szinten. (alfa=0.05, c 2tabla=3.84)
3. Egy kísérlet során kiderült, hogy két egyetemi csoportban a fiúk közül 7-en dohányoznak, 8-an nem. A lányok közül 28 a dohányos és 7 nem az. Hogyan tudnánk ezekből az adatokból eldönteni, hogy
az egyetemisták esetében a fiúk vagy a lányok között magasabb a dohányzók aránya? (95%-os szinten (alfa=0.05, c 2tabla=3.84)). Mi itt a nullhipotézis?4. Az egyetemi előadások elnéptelenedésének egyik szomorú megfigyelője úgy látta, hogy a fiúk kevésbé járnak órákra, mint a lányok. 30 fiúból mindössze 10 járt rendszeresen előadásokra, míg 90 lány közül éppen a fele. Alátámasztják ezek az adatok a lányok szorgalmasabb óralátogatását? (alfa=0.05, c
2tabla=3.84)) Mi itt a nullhipotézis?5. Két gyógyszert hasonlítottak össze mellékhatások szempontjából, 60 önkéntes pacienst véletlenszerúen soroltak be a két kezelés valamlyikébe. Független-e a mellékhatás attól, hogy melyik gyógyszerről van szó?
|
Mellékhatás volt |
Mellékhatás nem volt |
|
|
Drug A |
10 |
20 |
|
Drug B |
5 |
25 |
Megoldások
Adattípusok
1. Milyen adattípusok vannak aszerint, hogy milyen tulajdonságot képviselnek?.kvalitatív, kvantitaív...
Mi a különbség a nominális és ordinális változók között? .a nominális kategóriáit csak a nve különbözteti meg, az ordinális kategóriái kőzőtt van egy rendezés.....................................
Mondjon példát nominális változóra ......név, születési hely, vércsoport..............................................
Mondjon példát ordinális változóra .vizsgajegy, PH, betegség fokozatai................................................
Mondjon példát bináris (dichotóm) változóra ....nem....................................................................
2. A következő felje
gyzés egy eset orvosi jelentésének része"A paciens 32 éves gazdálkodó, feleségével és 2 gyermekével együtt Kiskundorozsmán lakik. A fő panasza lázas állapot az utóbbi 3 hónapban. A fehérvérsejtszáma 8700 és az urin analízis eredménye normál."
Képezzen változókat a következő szempontok szerint!
A változó neve Adattípusa A paciensre vonatkozó értéke
kor................. .folyt. vagy ordinális 32.....................................
.nem............... nominális......... férfi.................................
..fvs.................... folytonos.................. 8700.....................................
...................... .................. .....................................
Valószínűség
1: a) P(X=1)=1/6; b) P(X>1)=5/6; c) P(1<X<4)=1/3
2. Elemi események: FF,II, FI, IF. Annak a valószínűsége, hogy mindkét dobás írás, 1/4?
3.:
a) fej és páros dobás a kockával 3/12
b) fej vagy páros dobás a kockával 6/12
c) fej és 5-ös dobás 1/12
d) fej vagy 5-ös dobás 2/12
e) 4-es vagy 6-os dobás. 4/12
4. A és B, C és D, A és D kizáró események
5. A relatív gyakoriságok: E: x<26: : 2/15, F: x=31, 2/15 G: 26<x<31? 8/15
A legtöbb a normális vérnyomású ebben a mintában.
a) -átlag: 2.0000 medián:2.0000 stddev.3.1623 terjedelem:8.00
b) átlag:3.2500 medián:3.0000std.dev:1.5000 terjedelem:3.00
c) átlag:2.6667 medián:3.0000 std.dev:1.8619 terjedelem:5.00
d) átlag:1003.25 medián:1003 std dev: 1.5000 terjedelem: 3.00
3. A második átlag= (-1)*az első átlag, a standard devációk azonosak
4. Átlag(Y)=Átlag(X)+60, a standard devációk azonosak
5. átlag: 5. 5.0000 medián: 5.5000 std,dev:2.1602 terjedelem:5.00
5.5+2*2.16=5.5+4.32=9.32, nincs 2 standard deviációnál távolabbi elem az átlagtól.
6. Például: 1,1,1,1,1 vagy 3,3,3,3,3.
7. se=sd/Ö n=5.6/4=1.4
Konfidencia intervallum, t-próbák
Konfidencia intervallum a populáció átlagára ismeretlen szórás esetén: átlag ± ttabla*se
12 ± 2.13*1.4=12 ± 2.982 . Az intervallum: (9.018,14.982)
Ha a minta átlaga 12, mit tudunk mondani az átlag megbízhatóságáról (a =0.05, ttabla=2.13) ?
2. Egy vizsgálatban 10 egészséges nő systolés vérnyomását mérve, az átlagra 119-et, a standard deviációra 2.1-et kaptak.
b) Konfidencia intervallum a populáció átlagára ismeretlen szórás esetén: átlag ± ttabla*se
119 ± 2.26*0.664=119 ± 18.264. Az intervallum: (99.736,138.264)
c) A szabadságfok 10-1=9
3. A próbastatisztika t=különbség-átlag/SE=6/4.65=1.29
1.29<2.57, a különbség nem szignifikáns 95% -os szinten
4. A próbastatisztika t=különbség-átlag/SE=0.7/0.34=2.058
2.058<2.78,, a különbség nem szignifikáns 95% -os szinten
5. Feltéve, hogy a minták normális eloszlású populációból származnak, milyen próba alkalmas a kérdés eldöntésére? ..2 mintás t-próba.................................
Az átlagok közötti különbség szignifikáns:t=6.66, df=16, p<0.001. Ezt az eredményt a varianciák egyenlősége alapján végeztük el ( A varianciák nem különböznek:, p=0.939>0.05). A kezelés hatásos volt. 6. Mi a nullhipotézis?.A testsúlyok átlagai azonosak a szegedi és debreceni lányok populációjában..........
Mennyi a szabadságfok? ... 56+40-2=94............................
A p-érték p=0.136
Van-e szignifikáns különbség a két populáció átlaga között 95%-os szinten?.mincs
Miért?.................p>0.05..........................................................................................................................
Korreláció
A korreláció t-értéke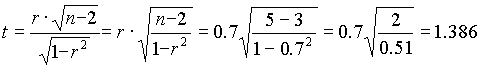 
.A szab.fok:.5-3=2.
...1.386<3.182, a korreláció nem szignifikáns 95 %-os szinten......
|
Dohányzik |
Nem dohányzik |
Összesen |
|
|
Fiú |
10 |
20 |
30 |
|
Lány |
15 |
15 |
30 |
|
Összesen |
25 |
35 |
60 |
Chi-négyzet próbák
1. A nullhipotézis: a dohányzás független a nemtől. c 2=(10*15-15*20)2*60/(25*35*30*30)=1.714<3.84.
A nullhipotézist nem tudjuk elvetni, a különbség nem szignifikáns 95%-os szinten.
2.A nullhipotézis: az elégedettség független a fizetéstől
. c 2=3.75<3.84,nincs elegendő információnk a nullhipotézis elvetéséhez, bár látható, hogy “majdnem” szignifiáns a különbség.5. c 2=2.22<c 2table=3.84,a különbség nem szignifikáns. Nincs elegendő informácink annak kimutatásához, hogy a B gyógyszer jobb, 95% -os szinten.
Adatbevitel az SPSS rendszerbe billentyűzetről és más rendszerekből
SPSS program indítása:
-Az SPSS program ikonjára kettőt kattintunk, erre elindul az SPSS program.
-A Start/Programok menüből kiválasztjuk az SPSS 8.0 for Windowst
Az SPSS program ablakai
Alkalmazás-ablak (menüsor). Itt lehet file-ok megnyitása, statisztikai eljárások, vagy a rendszer más lehetőségei közül választani.
Adat-ablak, a tetején eredetileg a Newdata felirat jelenik meg. Itt lehet új adatfile-okat létrehozni, vagy a meglevőket módosítani. Egyszerre csak egy adatfile lehet nyitva.
Output-ablak. Ebben láthatók a számítások, futtatások eredményei, szöveges információk. A benne levő szöveg módosítható vagy menthető. Egyszerre több output ablak is nyitva lehet.
Chart-ablak. Az ábrákat módodítani és menteni lehet.
Syntax-ablak. Az SPSS program parancsokkal dolgozik. A parancsokat ebbe az ablakba lehet beírni, majd futtatni. Mivel az SPSS for Windowsnak nagyon jól használható menürendszere is van, ezért ez a parancs-ablak csak rutinos felhasználók számára ajánlott. A menürendszer használata során a kiválasztott tevékenységet a "paste" funkció segítségével lehet parancs formájában a syntax-ablakba áttenni. Egyszerre több syntax ablakot is megnyithatunk.
Aktív ablak: a jelenleg kiválasztott ablak. Ha több ablak van megnyitva a képernyőn, akkor úgy válthatunk az ablakok között, hogy egyszerűen belekattintunk a kívánt ablakba. Ha nem látszik a keresett ablakunk, akkor vagy minimalizáljuk a többi ablakot, vagy rákattintunk a menüsor "Ablak" vagy "Window" szavára, ahol megjelenik az összes nyitott ablak neve, ezekből választhatunk.
Adatbevitel az SPSS rendszerbe, file-ok mentése
Az adatfile szerkezete
Az SPSS adafile-ban a sorok az eseteknek (megfigyeléseknek), az oszlopok változóknak felelnek meg. A cellák az adott változónak az adott megfigyelésre vonatkozó értékét tartalmazzák. Üres adat (missing value) esetén a cellában egy pont (.) jelenik meg.
A változónak lehet nevet adni, mely maximum 8 karakterből állhat.
A változók fajtái:
Cimkék:
Variable label: ha nem elég a 8 karakter a változó jellemzésére, a változó cimkéjében megadhatunk egy hosszab szöveges jellemzést
Value Label: numerikus változók egyes értékeit megcímkézhetjük. Pld. a NEM nevű változó 1-es értékéhez hozzárendelhetjük a "Férfi", 2-es értékéhez a "Nő" címkét.
Új adatfile létrehozása
·
Válasszuk ki a File menü New funkcióját.·
Válasszuk a Data-t az almenüből·
Definiáljuk a változókat.·
Írjuk be az adatokat.
Létező adatfile megnyitása
·
Válasszuk ki a File menü File funkcióját.·
Válasszuk az Open-t az almenüből·
Válasszuk ki az adattípust a File Type (file típusa) szerint .·
EXCEL file esetén válasszuk a *.xls kiterjesztésű file-okat.
EXCEL adatfile megnyitása
Az SPSS 6.1. verziója csak a 4.0-s EXCEL formátumot ismeri fel. Ezért, ha 5.0-s EXCEL-t használunk, az adatainkat mentsük el 4.0-s EXCEL munkalapként is. A legkedvezőbb, ha az SPSS által használt változóneveket az EXCEL táblázat első sorába beírjuk még az EXCEL-be. Az SPSS-be való beolvasásnál viszont ne felejtsük el a Read Variable Names-nél lévő kockát ki x-elni.
Az SPSS 8.0-s verziója ugyancsak 4.0-s Excel formátumot fogad, ha a File/Open menüből szeretnénk beolvasni. Viszont ha a File/Database Capture/New Query menüt használjuk, akkor későbbi verziójú Excel File-okat is be tudunk olvasni.
Változók definiálása
·
Az adat-ablakba lépjünk át.·
Kattintsunk duplán az első nem használt oszlop tetejére. Ha már létező változót szeretnénk újra definiálni, e változót tartalmazó oszlop tetejére kattintsunk kettőt.·
Alternatív módszer: kattintsunk akárhová az oszlopban és válasszuk a Data menüből a Define Variable funkciót.·
Írjuk be a változó nevét a Variable Name boxba.·
A változók alapfeltételezés szerint numerikus változók. Ha a változó nem számszerű értékeket fog tartalmazni, akkor a típusát meg kell változtatnunk String vagy egyéb típusúnak a Define Variable párbeszéd-ablakban. Ugyanitt megváltoztathatjuk vagy definiálhatjuk a változó típusát, címkéjét, hiányzó adatait és a formátumát.
Az adatok szerkesztése egy cellán belül
Az adatok értékét megváltoztathatjuk, törölhetjük, vagy átírhatjuk részben vagy egészben.
·
Válasszuk ki a módosítani kívánt cellát·
Írjuk be az új értéket.·
Nyomjuk meg az Entert.
Esetek vagy változók törlése
·
Egy eset (sor) törléséhez válasszuk ki a törlendő sort (a sor sorszámára klikkelve), majd nyomjuk meg a Del billentyűt vagy a Cleart az Edit menüből. A kitörölt sor alatti esetek eggyel feljebb kerülnek.·
Egy változó (oszlop) törléséhez válasszuk ki a törlendő oszlopot (az oszlop tetejére klikkelve), majd nyomjuk meg a Del billentyűt vagy a Cleart az Edit menüből. A kitörölt oszloptól jobbra levő változók eggyel balra kerülnek.
Kivágás, beillesztés és a Windows egyéb funkciói értelemszerűen használhatók.
Adatfile mentése: Save As (Data File)
Ha az adat-ablakban vagyunk, a File menü Save As almenüjében a következőket tehetjük:
·
Meghatározhatjuk a menteni kívánt file nevét: írjuk be a menteni kívánt adatfile nevét a Name boxban. Ez a box tartalmazza az adott típushoz tartozó kiterjesztésű fileneveket. Ebből a listából választhatunk, vagy új nevet írhatunk be.·
Meghatározhatjuk a menteni kívánt file helyét: a megfelelő Directory kiválasztásával.·
Meghatározhatjuk a menteni kívánt file típusát: a List Files of Type melletti nyílra kattintva a következő lehetőségek közül választhatunk:SPSS *.sav
Excel *.xls
SYLK *.slk
SPSS/PC+ *.sys
1-2-3 Release 2.0(WK1)
1-2-3 Release 3.0(WK3)
1-2-3 Release 1A(WKS)
dBASE II *.dbf
dBASE III *.dbf
dBASE IV *.dbf
SPSS Portable *.por
Tab delimited *.dat
Fixed ASCII *.dat
Eredmények elmentése: Save As (Output File)
Ha az output-ablakban (Output Navigator) vagyunk, a File menü Save As almenüjében ugyanúgy elmenthetjük az eredményeinket. Alapfeltételezésként *.spo kiterjesztést kapnak a file-ok.
A File/Export menü segítségével szüvegfile-ba (*.txt), vagy HTML file-ba menthetők az eredmények.
II/1.A. Folytonos változók jellemzése: hisztogram, boxplot, mintabeli jellemzők Az SPSS használata mintabeli jellemzők kiszám
Gyakoriságok, hisztogram vagy oszlopdiagram készítés: Statistics/Summarize/Frequencies
Mintabeli jellemzők egy adott változóról:
Statistics/Summarize/Frequencies vagy Statistics/Summarize/Descriptives vagy Statistics/Summarize/ExploreMintabeli jellemző változők csoportjairól:
Statistics/Summarize/Explore vagy Statistics/Compare Means/Means
A1. A BANK.SAV file-ban vizsgáljuk a SALBEG változót (kezdeti fizetés).
File beolvasás:
GET
FILE='KERD98.SAV'.
EXECUTE .
Milyen típusú változó?
a) Nominális - ordinális - kvantitatív
b) Diszkrét - folytonos
Hogyan lehet jellemzeni?
A1.a) Készítsen hisztogramot a SALBEG változóról. Jellemezze a kapott eloszlást.
GRAPH
/HISTOGRAM(NORMAL)=salbeg .
Mennyire szimmetrikus?................................
Ferde-e és merre?..........................................
Melyik fizetési kategória a leggyakoribb?.....................
A1.b.) Számoljon mintabeli jellemzőket a SALBEG változóból.
FREQUENCIES
VARIABLES=salbeg
/STATISTICS= MEAN STDDEV SEMEAN MEDIAN MINIMUM MAXIMUM.
Elemszám:.........
Átlag:............
Standard deviáció:............
Standard error:...............
Medián:.......................
Minimum:......................
Maximum:......................
SALBEG Beginning salary
Mean 6806.435 Std err 144.604 Median 6000.000
Std dev 3148.255 Minimum 3600.000 Maximum 31992.000
Valid cases 474 Missing cases 0
Mindezek alapján mennyire találja szimmetrikusnak az eloszlást és miért?
Mekkorának találja a standard deviációt? Mi az oka?
A1.c.) Számítsuk ki a mediánt, átlagot és szórást nemenként!
Mit jelent az átlag, és mit jelent a medián? Mi befolyásolja a nagyságukat?
USE ALL.
COMPUTE filter_$=(sex = 1).
VARIABLE LABEL filter_$ 'sex = 1 (FILTER)'.
VALUE LABELS filter_$ 0 'Not Selected' 1 'Selected'.
FORMAT filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE .
FREQUENCIES
VARIABLES=salbeg
/STATISTICS= MEAN STDDEV SEMEAN MEDIAN MINIMUM MAXIMUM.
USE ALL.
COMPUTE filter_$=(sex = 2).
VARIABLE LABEL filter_$ 'sex = 2 (FILTER)'.
VALUE LABELS filter_$ 0 'Not Selected' 1 'Selected'.
FORMAT filter_$ (f1.0).
FILTER BY filter_$.
EXECUTE .
FREQUENCIES
VARIABLES=salbeg
/STATISTICS= MEAN STDDEV SEMEAN MEDIAN MINIMUM MAXIMUM.
A1.d.) Számítsunk átlagot, szórást a SALBEG változóból nemenként
EXAMINE
VARIABLES=salbeg BY sex
/PLOT NONE
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
Ez a paranc
s nagyon sok statisztikai jellemzőt kiszámol. Keressük meg az átlagot és a standard deviációt, ellenőrizzük, hogy ez ugyanaz, mint amit az előbb kiszámoltunk.A program kiszámolja a következőket is:
Skewness 2.8529.(Ferdeség) Ez az eloszlás ferdeségére utal (0 esetben szimmetrikus az eloszlás, és minél nagyobb pozitív szám, annál jobban ferde az eloszlás jobbra)
A ferdeségre az átlag és a medián viszonya is utal. Melyik nagyobb és miért? .............
Kurtosis 12.3902 (Lapultság). A normálishoz képest csúcsosabb eloszlások esetén ez a lapultság pozitív, a laposabb eloszlások esetén negatív, normális eloszlás esetén 0.
Keletkezik egy un. Stem&Leaf diagram is, ez 90 fokkal elforgatva mutatja az eloszlás alakját.
A program rajzolt egy boxplotot is, ez is mutatja, milyen sok "kilógó" érték van.
A2. Nézzük meg, hogy az EXPLORE menüben mit lehet változtatni.
a)A Statistics ablakra rákattitva látjuk, hogy a Despcriptive (leíró statisztikák) be vannak xüelve, a többivel ne törődjünk.
b)A Plot ablakra rákattitva látjuk, hogy mi van kijelölve. Ezeket megváltoztathatjuk, így több vagy kevesebb ábrát készít a program.
c) A Factor list nevű ablak jelenleg üres. Ha ide valamelyik kategórikus változót bevisszük, akkor ennek a változónak a csoportjai szerint fogja meg
tenni a kijelölt vizsgálatokat.Vizsgáljuk meg a kezdeti fizetéseket nemek szerint. Hogy változik az eloszlás? Mi jellemző az átlagokra?
A3. Olvassuk be a DOLG.SAV file-t. Vizsgáljuk meg az EXPLORE paranccsal a SYSTOLES és a LAZ2 változókat NEMenként. Mennyire " hasonlít" az eloszlás a normálishoz?
Számolja ki (kézzel, vagy a Windowsban levő kis számológéppel) az átlag + 2-szeres standard deviációt, illetve az átlag - 2-szeres standard deviációt. Mennyire igazolják az így kapott értékek a normalitás
t?File beolvasás:
GET
FILE='KERD98.SAV'.
EXECUTE .
Mit mutat a ferdeség és a lapultság?
Mi a standard deviáció jelentése?
Mi a standard error jelentése?
Mi befolyásolja a szórások nagyságát?
EXAMINE
VARIABLES=laz2 systoles BY nem
/PLOT NONE
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
A4. Számítsunk mintabeli jellemzőket a következő adatokból, az eredményt írjuk ide a lapra:
68 69 70 70 70 71 71 71 72 72 72 73 73 74 75
Elemszám:.........
Átlag:............
Standard deviáció:............
Standard error:...............
Medián:.......................
Minimum:......................
Maximum:......................
Mindezek alapján mennyire találja szimmetrikusnak az eloszlást és miért?
Mi a terjedelem?
Javaslat:Ehhez az adatokat be kell írni. Rákattintunk az adat ablakra, majd File/New/Data. Erre keletkezik egy üres adatablak, ahova egymás alá be kell írni a fenti számokat. A változó neve var00001 lesz. Ha erre a szürke mezőre kettőt rákattintunk , megjelenik egy ablak, ahol el lehet nevezni a változót. Adjunk neki valami nevet, pld. "adat". Ezután a szokásos módon számolhatjuk ki a mintabeli jellemzőket a Frequency-vel vagy az Explore-ral.
FREQUENCIES
VARIABLES=adat
/STATISTICS= MEAN STDDEV SEMEAN MEDIAN MINIMUM MAXIMUM.
A5. Képezzünk csoportokat a fenti mintából.! Tegyük fel, hogy az első adat fiútól származik, a második lánytól, stb. Írjuk be ezt egy új változóba, melyet nevezzünk el "nem"-nek. Számítsuk ki az átlagokat és a szórásokat nemenként. Mentsük el az adatokat KISADAT.SAV néven a saját könyvtárunkba.
EXAMINE
VARIABLES=adat BY nem
/PLOT NONE
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
Mentés:
SAVE OUTFILE='C:\SPSS\KISADAT.SAV'
/COMPRESSED.
A6. Rajzoljunk átlag-szórás diagramot és box diagramot az előbbi átlagokról.
Milyen esetben érdemes a box-diagramot használni; és milyen esetben érdemes átlag-szórás diagramot?
Átlag-szórás diagram:
GRAPH
/ERRORBAR( CI 95 )=adat BY nem
/MISSING=REPORT.
Box diagram:
EXAMINE
VARIABLES=adat BY nem /PLOT=BOXPLOT/STATISTICS=NONE/NOTOTAL
/MISSING=REPORT.
A7. Számítsunk ki a következő mintabeli jellemzőket a KERD97 file testsúly, valamint testmagasság adataiból.
File beolvasás:
GET
FILE='KERD98.SAV'.
EXECUTE .
elemszám........................
átlag..................................
szórás.................................
medián................................
minimum............................ maximum...........................
FREQUENCIES
VARIABLES=magassag, suly
/STATISTICS= MEAN STDDEV SEMEAN MEDIAN MINIMUM MAXIMUM.
Mit jelentenek a fenti jellemzők? Ezek alapján mennyire tartja szimmetrikusnak az eloszlást?
A8. Számítsunk átlagot és szórást a testmagasságokból nemenként, és értelmezzük az eredményt.
EXAMINE
VARIABLES=magassag BY nem
/PLOT NONE
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
Értelmezés:
A9. Olvassa be a TANULO.SAV file adatait, mely középiskolás tanulók adatait tartalmazza. A számítások eredményét írja a lapra. A JSULY nevű változóban vannak a tanulók jelenlegi testsúlyai vannak. Jellemezze a testsúly változó eloszlását a megfelelő mintabeli jellemzők kiszámításával és értelmezze az eredményeket. Magyarázza el, mi a jelentése a kiszámított jellemzőknek. Készítsen grafikont, amely a testsúlyok eloszlását mutatja. Milyennek találja az eloszlást?
File beolvasás:
GET
FILE='TANULO.SAV'.
EXECUTE .
Általánosan:
FREQUENCIES
VARIABLES=jsuly
/STATISTICS= MEAN STDDEV SEMEAN MEDIAN MINIMUM MAXIMUM.
A10. A JSULY nevű változóban vannak a tanulók jelenlegi testsúlyai vannak. Jellemezze a testsúly adatokat a megfelelő mintabeli jellemzők kiszámításával, nemenként és értelmezze az eredményeket. Magyarázza el, mi a jelentése a kiszámított jellemzőknek. Készítsen grafikont, amely a testsúlyok nemenkénti eloszlását mutatja. Magyarázza el röviden, mit mutat a grafikon.
Nemenként:
EXAMINE
VARIABLES=jsuly BY nem
/PLOT NONE
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
II/1.B. Kategorikus adatok jellemzése
(Gyakoriság, relatív gyakoriság, oszlopdiagram, kördiagram)
B1. Olvassuk be a kis példa-kérdőív adatait (KISKERD.SAV)! Nézzük meg a nemek és az iskolai végzettségek gyakoriságait! Készítsünk oszlopdiagramot a gyakoriságokról. Az eredménylistát mentsük el a GYAK.SPO file-ba.
Megoldás
Adatfile beolvasása:
A File sorra rákattintok. Erre megjelenik egy új menü. Ebben tovább kijelölöm az Open-t, majd a Data-t. Az ilyen menüsorozatot a továbbikakban így jelölöm: File/Open/Data/. Erre megjelenik egy párbeszéd-ablak.
Itt be kell állítani, hogy melyik egységről akarok olvasni. Ehhez a Drives melleti kis nyílra kell kattintani, ha nem jó helyen vagyunk. A megfelelő Drive-ot úgy tudjuk kiválasztani, hogy a megfelelő sorra ráállunk, és kattintunk.
A file-nevek listájából ki kell választani hasonlóképpen a keresett file-nevet, vagy a File keretbe beírni a billentyűzetről a file-nevet.
OK (ra klikkelni ).
Parancsmódban:
File beolvasás:
GET
FILE='KISKERD.SAV'.
EXECUTE .
Gyakoriságok készítése.
Ehhez A FREQUENCIES eljárást kell futtatni: Statistics/Summarize/Frequencies.
A FREQUENCIES program futtatása:
Párbeszéd-ablak: a változók listája van felsorolva a balodalon. A megfelelőre rákattintok és utána a nyílra. Erre a kiválasztott változó átkerül a jobboldali ablakba (Variables). Egyszerre több változó is kijelölhető.
Display frequency tables: Ha ki van x-elve, akkor a változó minden egyes értékének az előfordulását ki fogja írni. (Gyakoirási megoszlás).
Statistics: ha erre ráklikkelek, egy újabb ablak jön be, melyben ki lehet jelölni, hogy milyen statistzikákat számoljon.
Charts: itt ki lehet jelölni, hogy készítsen-e grafikont és ha igen, milyet.
Format: a megjelenés formátumát lehet itt beállítani.
Esetünkben:
Statistics/Summarize/Frequencies/Charts/Bar chart/Continue/OK.
Az output mentése:
Beállok az output ablakba, és File/Save/, a megjelenő ablakban beállítom a Drive-ot és a könyvtárat, és
beírom a file-nevet.A grafikon
Ha kétszer rákattintok a grafiknra, akkor a grafikon szerkesztő ablakba kerülök. Itta grafikonon mindenféle módosítások hajthatók végre, ha kész van, az ablakot be kell zárni.
B2. Olvassa be a KERD94.SAV file-t. Nézze meg a vizsgajegyek eloszlását: készítsen oszlopdiagramot a vizsgajegyekről. Készítsen oszlopdiagramot a vizsgajegyekről nemenként is. Látható-e valami különbség a fiúk és lányok eredményei között? Véleménye szerint a látható különbség lényeges, vagy elhanyagolható?
GET
FILE='KERD94.SAV'.
EXECUTE .
Általános megoszlás
GRAPH
/BAR(SIMPLE)=COUNT BY vizsga
/MISSING=REPORT.
Nemenkénti megoszlás
GRAPH
/BAR(GROUPED)=COUNT BY vizsga BY nem
/MISSING=REPORT.
B3. Alakítsa át az oszlopdiagramot kördiagrammá. Mit tapasztal? (GALERY/PIE/REPLACE)
B4. Készítsen oszlopdiagramot a vizsgajegyekről, de most a gyakorlati jegyek függvényében. Értelmezze a látott eredményt.
GRAPH
/BAR(SIMPLE)=N(vizsga) BY gyakjegy
/MISSING=REPORT.
B5. Olvassa be a BANK.SAV file adatait. Itt a JOBCAT nevű változóban 1-7-ig kódolva találhatók különböző munkaköri kategóriák. Adja meg az egyes kategóriák gyakoriságait, írja ide, melyikből volt a legtöbb:
FREQUENCIES
VARIABLES=jobcat.
Kategória.................Gyakoriság.............Százalék......
Mi a gyakoriság és mi a relatív gyakoriság? Mi a köze a valószínűséghez?
..........................................................................................................................................
Milyen változó a JOBCAT? A megfelelő választ húzza alá
a) Nominális - ordinális - kvantitatív
b) Diszkrét - folytonos
Milyen ábrá(ka)t lehet készíteni a gyakoriságok ábrázolására?
........................................................
B6. Készítsen kördiagramot a JOBCAT nevű változó gyakoriságairól! (Graph/Pie/Define/ és az ablakban a jobcat változót átnyilazzuk a Define Slices by ablakba, OK).
GRAPH
/PIE=COUNT BY jobcat
/MISSING=REPORT.
B7. Olvassa be a TANULO.SAV file adatait, mely középiskolás tanulók adatait tartalmazza.
A tanulókat megkérdezték, hogy mennyire rettegnek az elhízástól. A válaszokat az EAT4 nevű változóban találjuk, 1-5-ig kódolva a következőképpen. 1: soha, 2: ritkán, 3: néha, 4: gyakran 5: nagyon gyakran, 6: mindig. Jellemezze ennek a változónak az eloszlását a megfelelő grafikonnal, és számítással, melynek az eredményét írja ide a lapra. Milyennek találja az eloszlást?
Megoszlás:
FREQUENCIES
VARIABLES=eat4 .
Grafikus megoszlás:
GRAPH
/BAR(SIMPLE)=COUNT BY eat4
/MISSING=REPORT.
B8. A TANULO:SAV file-ban az APIS nevű kategorikus változóban kódolva található az apa iskolai végzettsége. Jellemezze ennek a változónak az eloszlását a megfelelő grafikonnal, és számítással, melynek az eredményét írja ide a lapra. Milyennek találja az eloszlást?
FREQUENCIES
VARIABLES=apis
/STATISTICS=STDDEV MINIMUM MAXIMUM SEMEAN MEAN MEDIAN MODE SKEWNESS SESKW
KURTOSIS SEKURT .
Az SPSS alapjai
C1. Írja be a következő adatokat az az SPSS rendszerbe, és mentse el a file-t a saját könyvtárába. Milyen kiterjesztésű file keletkezik?
CSOPORT VÉRNYOMÁS
1 120
1 130
1 125
1 115
1 120
2 130
2 140
2 150
2 135
2 180
C2. Lássa el cimkékkel Csoport nevű változót: 1 = kontroll, 2 = beteg, és így mentse el az adatfile-t (rá a régire).
C3. Készítsen pontdiagramot és boxplotot a fenti adatokról. A grafikont színezze át, adjon neki címet, és változtassa próbáljon meg egy-két változtatást tenni. Mentse el a keletketett grafikont PROBA.CHT néven a saját könyvtárába.
Minta1: Olvassa be a KERD98.SAV file adatait. Számoljon mintabeli jellemzőket a testsúly adatokból. (SULY, SULYELSO, IDEALSLY)
A SULY változó jellemzése
A file beolvasása:
GET
FILE='KERD98.SAV'.
EXECUTE .
Leíróstatisztika:
FREQUENCIES
VARIABLES=suly
/STATISTICS= MEAN MEDIAN MODE STDDEV SEMEAN .
Elemszám: 43
Átlag:. 60.9535
Medián: 59
Modusz:60
Standard deviáció: 11.586
Standard error: 1.767
Feltéve, hogy a testsúlyok normális eloszlású populációból származnak, adjon 95%-os és 99 %-os konfidencia intervallumot a testsúlyok populáció-átlagára.
95%-os konf. int a SULY változóra: (57.388 , 64.519)
T-TEST
/TESTVAL=0
/MISSING=ANALYSIS
/VARIABLES=suly
/CRITERIA=CIN (.95) .
99%-os konf. int a SULY változóra: (56.186 , 65.721)
T-TEST
/TESTVAL=0
/MISSING=ANALYSIS
/VARIABLES=suly
/CRITERIA=CIN (.99) .
Mit jelent a konfidencia intervallum?
Eltér-e a testsúly várható értéke 70-től 95 %-os szinten?................
Miből állapította meg?
Megoldás:
Próba neve: egymintás t-próba
Nullhipotézis?
Alternatív hipotézis?
Parancs a Menű-b
en :Statistics/Compare Means/One-Sample T TestA SULY változó kiválasztása után a Test value-t 70-re kell beállítani vagy a Syntax ablakba beírni a következő parancsot:
T-TEST
/TESTVAL=70
/MISSING=ANALYSIS
/VARIABLES=suly
/CRITERIA=CIN (.95) .
Nullhipotézis: A SULY változó átlaga 70.
Alternatív hipotézis: A SULY változó átlaga eltér 70-től.
SPSS output:
One Sample t-tests
Number
Variable of Cases Mean SD SE of Mean
-----------------------------------------------------------------------
SULY Jelenlegi testsúlya 43 60.9535 11.586 1.767
-----------------------------------------------------------------------
Test Value = 70
Mean 95% CI |
Difference Lower Upper | t-value df 2-Tail Sig
-----------------------------------------------------------------------
-9.05 -12.612 -5.481 | -5.12 42 .000
-----------------------------------------------------------------------
t érték: -5.12
df: 42
p=0.000
Mivel a kapott p érték kisebb mint 0.05, ezért az alternatív hipotézist fogadjuk el.
Készítsen ábrát a testsúlyok átlagairól és a konfidencia intervallumokról.
EXAMINE
VARIABLES=suly /COMPARE VARIABLE/PLOT=BOXPLOT/STATISTICS=NONE/NOTOTAL
/MISSING=LISTWISE .
A SULYELSO, IDEALSLY változókra hasonlóan készíthető el a megoldás.
Minta2. Hasonlítsa össze a testsúlyváltozást (SULY, SULYELSO).
Van-e szignifikáns különbség a mostani és a jelenlegi testsúly átlagai között?...............
Mi a nullhipotézis?.....................
Mi alapján döntött?...........
Megoldás:
Próba neve: egymintás t-próba
Parancs a Menű-ben :
Statistics/Compare Means/Paired-Sample T TestA SULY, SULYELSO változó kiválasztása után OK gombra kell kattintani vagy a Syntax ablakba beírni a következő parancsot:
T-TEST
PAIRS= suly WITH sulyelso (PAIRED)
/CRITERIA=CIN(.95)
/FORMAT=LABELS
/MISSING=ANALYSIS.
Nullhipotézis: A SULY és SULYELSO változók különbsége 0.
Alternatív hipotézis: A SULY és SULYELSO változók különbsége eltér 0-tól.
SPSS output file:
t-tests for Paired Samples
Number of 2-tail
Variable pairs Corr Sig Mean SD SE of Mean
-------------------------------------------------------------------------------
SULY Jelenlegi testsúlya 61.7317 11.241 1.755
41 .952 .000
SULYELSO Testsúlya elsőéves korában
60.8780 10.748 1.678-------------------------------------------------------------------------------
Paired Differences |
Mean SD SE of Mean | t-value df 2-tail Sig
----------------------------------|--------------------------------------------
.8537 3.454 .539 | 1.58 40 .121
t érték: 1.58 df: 40 p=0.121
Mivel a kapott p érték nagyobb, mint 0.05, ezért a null hipotézist fogadjuk el.
A1. Olvassa be az AGE.SAV file adatait. Ebben a file-ban egyetlen változó van, amely 50, bizonyos betegségben meghalt személy életkor adatait tartalmazza. Állíthatjuk-e, hogy ebben a betegségben a halálozás átlagosan a 30 éves kor alatt következik be?
Végezze el a megfelelő próbát
Elemszám:.........
Átlag:............
Standard deviáció:............
Standard error:...............
Mi a nullhipotézis?.....................
Mi az alternatív hipotézis?.................
t érték........................
szabadságfok...............
p érték.........................
Következtetés
A2.Végezze el a fenti összehasonlítást nemenként. Vajon a fiúk és a lányok testsúlyai egyformán változtak? Változók csoportjai szerinti kiértékelés menete:
Data/Split File/Repeat analysis for each group/Nyíllal átvinni a NEM nevű változót a "Groups Based on" ablakba,/Sort file by grouping variables/OK.
A fenti parancssor hatására minden, ezután elvégzett akció a nemek csoportjaira külön-külön fog lefutni, mindaddig, amíg a vissza nem állítjuk a Data/Split File/Analyse all cases/OK paranccsal.
Fiúk
Jelenlegi testsúly átlaga ..............................szórása.................................
Elsőéves testsúly átl
aga.............................szórása.................................A próba neve:
Eredménye
Magyarázat
Lányok
Jelenlegi testsúly átlaga ..............................szórása.................................
Elsőéves testsúly át
laga.............................szórása.................................A próba neve:
Eredménye
Magyarázat
A3. Ismételje meg a fentieket a testmagasság adatokkal
A4. Ismételje meg a fentieket a KERD94.SAV file adatain
A5. Ismételje meg a fentieket a BANK.SAV file a kezdeti és a mostani fizetések adatain.
A6. Ugyanazokon az embereken vérnyomást mértek kétszer egymás után. Az eredmények a DOLG file systoles és systoles1 nevű változójában vannak. Ellenőrizzük azt a hipotézist, hogy a vérnyomás két mérésének várható értéke ugyanaz 95%-os szinten.
Sytoles átlaga............. szórása...............
Sytoles1 átlaga............. szórása...............
t érték .......... szabadságfok ........p érték...........
Mi itt a nullhipotézis?
Döntés indoklással...................
A7. Ugyanazokon az embereken lázat mértek kétszer egymás után. Az eredmények a DOLG file laz1 és laz2 nevű változójában vannak. Ellenőrizzük azt a hipotézist, hogy a láz két mérésének várható értékének különbsége=0 95%-os szinten.
A8. Vizsgáljuk meg a KERD98.SAV file adatai alapján, hogy volt-e szignifikáns változás a testsúlyokban 4 év alatt! A SULYMOST nevű változó a jelenlegi, a SULY1 pedig a tanulmányok kezdetén meglevő súlyokat tartalmazza. Egyformának tekinthető-e a két mérés várható értéke 99%-os szinten?
A9. Egy vérnyomáscsökkentő gyógyszert négy különböző betegen próbáltak ki, a következő eredménnyel:
Gyógyszer nélküli systolés vérnyomás: 190 180 220 220
Gyógyszerrel mért systolés vérnyomás: 110 150 150 190
A megfelelő t-próba
segítségével döntsünk, hogy hatásos-e a gyógyszer! (szignifikancia szint: 95%) Mi itt a nullhipotézis?
A10. Olvassa be a BEFAFTER.SAV file adatait. Ebben az első két változó egy diétás teszt eredményeit tartalmazza egy 12 hetes diéta előtt és után (testsúlyok) . Elegendő-e a bizonyíték arra, hogy a diéta hatásos volt?
Diéta előtti testsúly átlaga ..............................szórása.................................
Diéta utáni testsúly átlaga.............................szórása.................................
A próba neve:
Mi a nullhipotézis?.....................
Mi az alternatív hipotézis?.................
A próba eredménye
Magyarázat
A11.A BEFAFTER.SAV file Stage1 és a Stage2 nevű változói egy máik kísérlet artériás diastolés nyomás értékeit mutatja a kísérlet két stádiumában, ugyan azokon a pacienseken. Mondhatjuk-e, hogy az artériás diastolés nyomás értékek átlagai azonosak a két stádiumban?
A12. 6 ember trombocita tömegét mérték meg egy szivar elszívása előtt és után. Az adatok a következők:
Előtt: Után:
1.ember 25 27
2.ember 27 35
3.ember 29 42
4.ember 30 38
5.ember 43 58
6.ember 50 76
Van-e szignifikáns különbség az első és második mérések átlagai között? Végezze el a megfelelő próbát, a szignifikancia szint legyen 95%.
Minta. Olvassa be a KERD98.SAV file adatait. Hasonlítsa össze a testsúlyok átlagait nemek szerint. Van-e szignifikáns különbség a fiúk és lányok testsúlyainak átlagai között? Készítsen ábrát a testsúlyok átlagairól és a konfidencia intervallumokról!
Fiúk átlaga............... szórása....... elemszáma.......
Lányok átlaga............... szórása....... elemszáma.......
A próba neve:
Mi a nullhipotézis?.....................
Mi az alternatív hipotézis?.................
Mi a próba feltétele:............................................
A varianciák azonosságának ellenőrzése.......................................
A próba eredménye
t...............................................szab.fok:.....................................p............................................
Magyarázat
Megoldás:
GET
FILE='KERD98.SAV'.
EXECUTE .
A próba neve: kétmintás t-próba (STATISTICS/Compare Means/Independent-Samples T Test)
T-TEST
GROUPS=nem(1 2)
/MISSING=ANALYSIS
/VARIABLES=magassag
/CRITERIA=CIN(.95) .
Nullhipotézis: A fiúk és a lányok átlagos testmagassága azonos.
Alternativ hipotézis: A fiúk és a lányok átlagos testmagassága eltérő.
Mi a próba feltétele: A két csoport varianciái egyenlő legyen
A varianciák azonosságának ellenőrzése : F-test
Nullhipotézis: A csoportok varianciái azonosak.
Alternativ hipotézis: A csoportok varianciái nem azonosak.
Az F-próba eredménye: Levene's Test for Equality of Variances: F= .310 P= .580
Mivel a P= .580>0.05 ezért a varianciák azonosnak tekinthetők.
A t-próba eredménye:
Number
Variable of Cases Mean SD SE of Mean
-----------------------------------------------------------------------
MAGASSAG Testmagasság
fiú 14 182.4286 7.842 2.096
lány 47 167.6170 7.051 1.029
-----------------------------------------------------------------------
Mean Difference = 14.8116
t-test for Equality of Means 95%
Variances t-value df 2-Tail Sig SE of Diff CI for Diff
-------------------------------------------------------------------------------
Equal 6.73 59 .000 2.202 (10.405, 19.218)
Unequal 6.34 19.69 .000 2.335 (9.937, 19.686)
-------------------------------------------------------------------------------
Fiúk átlaga.:182.428 szórása:7.842 elemszáma.:14
Lányok átlaga:167.617 szórása:7.051 elemszáma.: 47
t=6.73 szab.fok:59 p: 0.000
Magyarázat
Mivel a varianciák azonsnak tekinthetők az F-test alapján, ezért a t-próba eredményét az Equal sorban talá
ljuk. Ez alapján nullhipotézisünket - A fiúk és a lányok átlagos testmagassága azonos - elvetjük és az alternatív hipotézist fogadjuk el.
Készítsen ábrát a testsúlyok átlagairól és a konfidencia intervallumokról!
EXAMINE
VARIABLES=magassag BY nem /PLOT=BOXPLOT/STATISTICS=NONE/NOTOTAL
/MISSING=REPORT.
B1. Olvassa be a LAZAROKT.SAV nevű filet. Az LPS nevű szer hatását vizsgálták többek között a fehérvérsejtszámra. A kísérleti állatokat véletlenszerűen két részre osztoták, az egyik rész nem kapott LPS-t (kontroll), a másik pedig kapott. Az OSSZFVS nevű változó tartalmazza a fehérvérsejtszámot, , az LPS pedig 0 és 1 -et,(0=kontroll, 1=LPS).
Mondhatjuk-e, hogy az LPS hat a fehérvérsejtszám alakulására?
B2. Olvassa be a BANK.SAV file adatait. Számoljon átlagot és szórást a kezdő fizetésekből (SALBEG) aszerint, hogy az illető fehér vagy fekete! (Azaz, a MINORITY nevű változó értékei szerint. Itt 0 kódolja a fehéret és 1 a feketét.)
Van-e szignifikáns különbség a fehérek és a feketék átlagai között?
Fehérek átlaga............... szórása....... elemszáma.......
Feketék átlaga............... szórása....... elemszáma.......
B3. Ismételje meg az előző eljárást a kezdő fizetésekre nemek szerint.
B4. Hasonlítsuk össze a KERD94 file-beli testsúly értékeket aszerint, hogy az illető eltörte-e a csontját valaha, vagy nem. Ezt úgy jelöltük, hogy a CSONT nevű változóba 1-est írtunk, ha igen, 2-est, ha nem törte el. A testsúly a SULYMOST nevű változóban van. Van-e szignifikáns különbség a várható értékek között 95%-os szinten? A szórások egyezésétől függően (ezt 95%-os szinten teszteljük) döntsünk!
1-es csoport elemszáma......testsúly átlaga.........szórása..........
2-es csoport elemszáma......testsúly átlaga.........szórása..........
t érték .......... szabadságfok ........p érték...........
Döntés indoklással...................
Mit jelent a szignifikáns (vagy nem szignifikáns) eredmény?
B5.Hasonlítsuk össze a KERD98 file-beli fiúk és lányok testmagasságát! Van-e szignifikáns különbség a várható értékek között 95%-os szinten? A szórások egyezésétől függően döntsünk 95%-os szinten!
Hús: 4.3 4.4 4.9 4.9 5.1 5.3 5.6
Gyümölcs-zöldség: 4.3 4.4 4.5 4.9 4.9 5 5.6
Az adatok a SZOKAS:SAV file-ban vannak. A csoportok kódjai a csoport nevű változóban vannak (1=hús. 2=zöldség), a cardiac output mért értékei a szív nevű változóban.
Van-e szignifikáns különbség a két speciálisan kezelt populációk átlagaiban 95% -os szinten?
B6. Hasonlítsuk össze a LANYOK.SAV file adatai alapján a jelenlegi testsúlyokat aszerint, hogy volt-e már levert időszaka az életében (SZOM változó). Kik a kövérebbek átlagosan, a szomorúak, vagy a vidámak? A varianciák egyezésétől függően (ezt 95%-os szinten teszteljük) döntsünk!
B7.Most azt nézzük meg, hogy a testsúly függ-e az evés szeretetétől, azaz, hasonlítsuk össze a testsúlyok átlagait (JSULY) két csoportban: akik szeretnek enni, és akik nem szeretnek enni. Mondhatjuk–e 5% hiba mellett, hogy akik szeretnek enni, azok átlagosan kövérebbek, mint akik nem szeretnek enni?
Minta. Hasonlítsuk össze a KERD94 file SULYMOST nevű változójának középértékeit aszerint, hogy milyen üdítőt szeret a legjobban! Van-e szignifikáns különbség 95 %-os szinten?
1-es üdítő(Coca Cola)csoport elemszáma.......átlaga.......
2-es üdítő(Fanta) csoport elemszáma.......átlaga.......
3-es üdítő(Sprite) csoport elemszáma.......átlaga.......
Döntés:p=.......
Mely csoportok között van szign. különbség?
Mi a megfelelő próba neve:
Feltételei:
Teljesülnek-e a feltételek:
Megoldás:
File megnyitása:
GET
FILE='C:\SPSS\KERD94.SAV'.
EXECUTE .
A próba neve: Egyszempontos variancia-analízis (STATISTICS/Compare Means/One-way ANOVA)
Paraméterek:
Dependent list: a vizsgált változó(k), esetünkben a SULYMOST változó;
Factor: A csoport változó, esetünkben az UDITO (1-3 érték beálítása a Define Range paranccsal történik)
Options: A leíróstatisztika (Descriptives) beállítása
Post Hoc: A páronkénti összehasonlítást végző módszer kiválasztása (LSD, Bonferoni,…)
ONEWAY
sulymost BY udito(1 3)
/RANGES=LSD
/RANGES=LSDMOD
/HARMONIC NONE
/STATISTICS DESCRIPTIVES
/FORMAT NOLABELS
/MISSING ANALYSIS .
Nullhipozés: A csoportok varianciái egyenlőek
Alternatív hipotézis: A varianciák között van különbség.
Analysis of Variance
Sum of Mean F F
Source D.F. Squares Squares Ratio Prob.
Between Groups 2 789.8128 394.9064 3.6632 .0297
Within Groups 86 9271.1310 107.8038
Total 88 10060.9438
Standard Standard
Group Count Mean Deviation Error 95 Pct Conf Int for Mean MINIMUM MAXIMUM
Grp 1 52 63.4423 11.1837 1.5509 60.3287 TO 66.5559 48.0000 90.0000
Grp 2 19 60.1579 10.5739 2.4258 55.0614 TO 65.2543 49.0000 97.0000
Grp 3 18 55.8889 7.1939 1.6956 52.3115 TO 59.4663 47.0000 70.0000
Total 89 61.2135 10.6925 1.1334 58.9611 TO 63.4659 47.0000 97.0000
1-es üdítő(Coca Cola)csoport elemszáma(Count) 52 átlaga(Mean) 63.442
2-es üdítő(Fanta) csoport elemszáma(Count) 19 átlaga(Mean) 60.157
3-es üdítő(Sprite) csoport elemszáma(Count) 18 átlaga(Mean) 55.888
Döntés:p=0.0297
Mely csoportok között van szign. különbség? Az 1-3 csoportok között.
(*) Indicates significant differences which are shown in the lower triangle
G G G
r r r
p p p
3 2 1
Mean UDITO
55.8889 Grp 3
60.1579 Grp 2
63.4423 Grp 1 *
C1. Az egészségükkel törődő emberek jobban szerethetik azokat a hot-dogokat, amelyek kecvesebb sót és kevesebb kalóriát tartalmaznak. A "HOTDOG" adatfile 54 hotdogkészítő cég készítményeinek sodium és kalória értékeit tartalmazza. A hotdogok típus szerint vannak osztályozva: marha, szárnyas és vegyes [beef, poultry, and meat (mostly pork and beef, but up to 15% poultry meat)]. Egyszempontos variancia analízissel tesztelhetjük, hogy vajon a szódium- és kalória mennyisége függ-e a hotdog típusától. (Forrás: Internet – http://lib.stat.cmu.edu/DASL)
A simple ANOVA model with type as the independent variable and calories as the dependent variable has an F-ratio of 16.074 , which is highly significant. Post-ANOVA analysis of group means shows that meat and beef hot dogs have approximately the same number of calories and poultry hot dogs generally have fewer calories than either beef or meat hot dogs. The same model with sodium as the dependent variable has an overall F-ratio of 1.78, which is not significant. None of the individual differences are significant.
Reference: Moore, David S., and George P. McCabe (1989). Introduction to the Practice of Statistics. Original source: Consumer Reports, June 1986, pp. 366-367.
Az adatok a HOTDOG.SAV file-ban találhatók, a változónevek a következők:
1. Type: Type of hotdog (1=beef, 2=meat, 3=poultry)
2. Calories: Calories per hot dog
3. Sodium: Milligrams of sodium per hot dog
C2. Olvassuk be a LANYOK.SAV adatafile-t. Az adatok egészséges középiskolás tanulólányok adatait tartalmazzák egy kérdőíves vizsgálat után.A tanulólányok étkezési szokásait, szociális helyzetét és deviáns magatartását, valamint ezek kapcsolatát vizsgálták. Ebben a file-ban a sok változó közül a következő változókat fogjuk vizsgálni:
|
AZON |
Azonosító szám |
|
. . . |
|
|
ALK |
Alkoholfogyasztás 2 társaságban iszom 3 rendszeresen iszom |
|
. . . |
|
|
JSULY |
Jelenlegi testsúlya |
|
... |
Hasonlítsuk össze a jelenlegi testsúlyokat is az alkoholfogyasztás szerint. (ALK) .Tehát vizsgáljuk meg, hogy abban a 3 csoportban, amely nem iszik alkoholt, társasági ivó és rendszeresen iszik, egyformák-e a testsúlyok populációbeli átlagai.
Szignifikáns esetben a páronkénti hasonlításokat végezzük Bonferroni módszerrel. Legyen a szignifikancia szint 95%.
C3. Állapítsuk meg variancia analízissel, hogy az alacsony születési súlyokat három csoportba osztva (1:< 1000 g ;2: 1000-2000 g és 3:2000-2500 g) csoportok között van-e eltérés a perinatális mortalitás között. Az adatok a TESZT2 file-ban találhatók: PERMORT a perinatális mortalitás változó és SULYCSOP a csoport-beosztást tartalmazó változó.
Mely csoportoknál van eltérés a Scheffé módszer alapján ?
C4. 23 túlsúlyos férfit három különböző módszerrel próbálnak lefogyasztani: diétával, mozgással vagy étkezési szokás módosításával. A súly változást két hónap után rögzítették. Az eredmények a következők:
Diétás csoport: 3 4 0 -3 5 10 3 0
Mozgás terápiás csoport: -1 8 4 2 2 -3
Étkezési szokás módosított csoport: 7 1 10 0 18 12 4 6 5
A negatív érték súlygyarapodást jelent!
Hasonlítsuk össze a módszereket! Mit állapíthatunk meg?
Minta. Rajzoljuk fel a KERD98 file-beli testsúly és testmagasság közötti lineáris kapcsolatot kifejezõ regressziós egyenest, adjuk meg az egyenes egyenletét és a korrelációs együtthatót, és számítsuk ki hogy a 160 cm testmagassághoz hány kg testsúly tartozik. Vajon szignifikáns-e a korreláció? Írjuk ki a megfelelõ statisztika értékét, amelynek alapján a kérdést eldöntöttük. Mi itt a nullhipotézis?
Megoldás:
File beolvasása:
GET
FILE='KERD98.SAV'.
EXECUTE .
Statistics/Regressio/Linear
Beállítások Y (Dependent) változó a SULY és az X (Independent) változó a MAGASSAG
REGRESSION
/DESCRIPTIVES MEAN STDDEV CORR SIG N
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT suly
/METHOD=ENTER magassag .
vagy
Statistics/Regressio/Curve Estimation
* Curve Estimation.
TSET NEWVAR=NONE .
PREDICT THRU END.
CURVEFIT /VARIABLES=suly WITH magassag
/CONSTANT
/MODEL=LINEAR
/PRINT ANOVA
/PLOT NONE.
Az SPSS output:
* * * * M U L T I P L E R E G R E S S I O N * * * *
Equation Number 1 Dependent Variable.. SULY Jelenlegi testsúlya
Block Number 1. Method: Enter MAGASSAG
Variable(s) Entered on Step Number
1.. MAGASSAG Testmagasság
Multiple R .77136
R Square .59499
Adjusted R Square .58813
Standard Error 8.35965
Analysis of Variance
DF Sum of Squares Mean Square
Regression 1 6057.21485 6057.21485
Residual 59 4123.14580 69.88383
F = 86.67549 Signif F = .0000
------------------ Variables in the Equation ------------------
Variable B SE B Beta T Sig T
MAGASSAG 1.053949 .113206 .771356 9.310 .0000
(Constant) -119.406407 19.389727 -6.158 .0000
End Block Number 1 All requested variables entered.
Korrelációs együttható (Multiple R) 0.77136
R-négyzet (R Square): 0.59499
Szignifikancia (7-es verziótól kiíródik)
Az egyenes egynlete (Y=B*X+Constant):SULY=1.053949*MAGASSAG-119.406407
Az egyenes egyenlete alapján 160 cm-es testmagasssághoz :
1.053949*160-119.406407=58.3229 kg-os testsúly tartozik.
Korreláció szignifikancia vizsgálata:
Nullhipotézis: A korrelációs együttható értéke nullával egyenlő.
Alternatív hipotézis: A korrelációs együttható értéke nem egyenlő nullával.
D1. Milyen függvény illik inkább a következő adatokra, lineáris vagy exponenciális ?
X: 0.1 1 2 3 4
Y: 1.9 3 3.9 9 16
Rajzoljuk ki a függvényt. Minek alapján döntött?
Megoldás:
Statistics/Regressio/Curve Estimation
* Curve Estimation.
TSET NEWVAR=NONE .
PREDICT THRU END.
CURVEFIT /VARIABLES=suly WITH magassag
/CONSTANT
/MODEL=LINEAR EXPONENTIAL
/PRINT ANOVA
/PLOT NONE.
D2
. Határozzuk meg a korrelációs együtthatót és írjuk fel a regressziós egyenes egyenletét a következő kétváltozós mintában:X: 2 4 6 8 10 13
Y: 1 4 5 8 9 14
A korrelációs együttható:
Mit fejez ki a korrelációs együttható nagysága (abszolút értéke) ?
Mit fejez ki a korrelációs együttható előjele ?
Szignifikáns-e a korreláció? p=
A regressziós egyenes egyenlete:
D3. Rajzoljuk meg a DOLGOZAT file-beli alacsony születési súly ( SZSULY) évenkénti változását(EVEK) leíró lineáris összefüggést kifejező regressziós egyenest!
Hány százalékos alacsony születési súlyú eset várható 1994-ben ?
D4. Egy brit felmérésben a háztartások dohányra illetve alkoholra történő kiadásaik közötti összefüggést vizsgálták Nagybritaania 11 különböző tartományában. Az alkohol és a dohányra költött összegek közötti szóródáasi diagram alapján vizsgáljuk meg a két változó közötti összefüggést. Van az adatok között egy "nem odaillő" (outlier): Northern Ireland . Vizsgáljuk meg a korrelációt és a regressziós egyenes egyenletőt az összes adat figyelembe vételével és Northern Ireland nélkül! (Forrás: Internet: http://lib.stat.cmu.edu/DASL)
Az adatok az ALKOHOL.SAV file-ban vannak. A változók a következők:
1. Region: Region of Great Britain
2. Alcohol: Average weekly household spending on alcoholic beverages in pounds
3. Tobacco: Average weekly household spending on tobacco products in pounds
D5. Olvassuk be a LANYOK.SAV adatafile-t. Az adatok egészséges középiskolás tanulólányok adatait tartalmazzák egy kérdőíves vizsgálat után.A tanulólányok étkezési szokásait, szociális helyzetét és deviáns magatartását, valamint ezek kapcsolatát vizsgálták. Ebben a file-ban a sok változó közül a következő változókat fogjuk vizsgálni:
|
AZON |
Azonosító szám |
|
. . . |
|
|
SZOM |
Volt-e levert időszaka életében : 1=igen, 2= nem , 9= nincs adat, hiányzó értéknek van kódolva, a számításoknál nem lesz figyelembe véve |
|
ONGY |
Öngyilkossági késztetés 1: sohasem volt, 2: foglalkoztam a gondolatával |
|
ALK |
Alkoholfogyasztás 2 társaságban iszom 3 rendszeresen iszom |
|
. . . |
|
|
JSULY |
Jelenlegi testsúlya |
|
KSULY |
Kívánatos testsúlya |
|
MAGAS |
Testmagasság |
|
ENNI |
Mennyire szeret enni 2 meglehetősen 3 közömbös 4 alig 5 egyáltalán nem 9 nincs válasz |
|
EVES |
Szeret-e enni , 1= igen 2=nem |
|
... |
|
|
EAT4 |
Rettegek, hogy elhízom (Milyen gyakran jut eszébe?) |
Vizsgáljuk meg a jelenlegi testsúly és a kívánatos testsúly közötti kapcsolatot. Függ-e a kívánatos testsúly értéke a jelenlegitől? Mivel tudja jellemezni az összefüggést?
Számítsa ki az egyenlet alapján 60 kg-os jelenlegi testsúly esetén a függő változó "jósolt" értékét!
Vizsgáljuk meg a jelenlegi testsúly és a testmagasság közötti kapcsolatot. Van-e (lineáris) kapcsolat a testsúly és a testmagasság között? Legyen a független változó a testmagasság.
Számítsa ki az egyenlet alapján 160 cm-es testmagasság esetén a függő változó "jósolt" értékét!
Minta 1. Vizsgáljuk meg, hogy a vizsgajegyek és gyakorlati jegyek függetlenek-e egymástól a KERD98.SAV file adatai szerint! Milyen próbát használ?:
Mi a nullhipotézis?
Melyik cellában van a legnagyobb gyakoriság?
Hányan voltak 3-asok mind gyakorlaton, mind a vizsgán?
szabadságfok (df)
p-érték
Várt gyakoriságokra vonatkozó feltétel teljesül-e
Értelmezés
Megoldás:
A próba neve: c 2
Nullhipotézis: A vizsgajegy függetlennek tekinthetö a gyakorlati jegytől
Alternatív hipotézis: A vizsgajegy függ a gyakorlati jegytől
File beolvasása:
GET
FILE='KERD98.SAV'.
EXECUTE .
Statistics/Summarize/Crosstabs…
CROSSTABS
/TABLES=gyakjegy BY vizsga
/FORMAT= AVALUE NOINDEX BOX LABELS TABLES
/STATISTIC=CHISQ
/CELLS= COUNT .
SPSS output
GYAKJEGY by VIZSGA
VIZSGA Page 1 of 1
Count |
|
| Row
| 2.00| 3.00| 4.00| 5.00| Total
GYAKJEGY --------+--------+--------+--------+--------+
3.00 | 1 | 2 | 2 | 2 | 7
| | | | | 11.7
+--------+--------+--------+--------+
4.00 | 2 | 6 | 4 | 3 | 15
| | | | | 25.0
+--------+--------+--------+--------+
5.00 | 6 | 9 | 8 | 15 | 38
| | | | | 63.3
+--------+--------+--------+--------+
Column 9 17 14 20 60
Total 15.0 28.3 23.3 33.3 100.0
Chi-Square Value DF Significance
-------------------- ----------- ---- ------------
Pearson 2.57246 6 .86027
Likelihood Ratio 2.61558 6 .85531
Linear-by-Linear .41338 1 .52026
Association
Minimum Expected Frequency - 1.050 Cells with Expected Frequency < 5 - 7 of 12 ( 58.3%)
Melyik cellában van a legnagyobb gyakoriság? Az 5-ös vizsga és 5-ös gyakorlati jegy (15)
Hányan voltak 3-asok mind gyakorlaton, mind a vizsgán? 2
szabadságfok (df): 6
p-érték: 0.86027
Értelmezés
A p érték alapján (p>0.05) a nullhipotézist fogadjuk el.
Minta2. 30 egyetemi hallgató lány közül 20 aktívan sportolt, míg ugyanannyi fiú közül csak 5. Állíthatjuk-e 95%-os szinten, hogy a lányok aktívabb sportolók? (Forrás: Hajtman Béla)
Adjuk meg a gyakorisági táblázatot:
|
Aktív |
Nem aktív |
Összesen |
|
|
Lányok |
|||
|
Fiúk |
|||
|
Összesen |
Végezzük el a megfelelő próbát, írjuk le a statisztikát, p-értéket, és a döntést 95 %-os szinten.
Megoldás:
|
Aktív |
Nem aktív |
Összesen |
|
|
Lányok |
20 |
10 |
30 |
|
Fiúk |
5 |
25 |
30 |
|
Összesen |
25 |
35 |
60 |
Az SPSS használata a feladat megoldáshoz:
A táblázat adatait -kivéve a sor, illetve oszlop összegeket- mátrixnak tekintjük a11=20, a12=10, a21=5, a22=25.
Az SPSS-ben létrehozunk egy új adattáblát, amely definiálja a 2x2-es mátrix-ot.
Az első változó - nevezzük SOR-nak a következő értékeket tartalmazza: 1,1,2,2.
Az második változó - nevezzük OSZLOP-nak a következő értékeket tartalmazza: 1,2,1,2.
Az harmadik változó - nevezzük ADAT-nak a következő
értékeket tartalmazza: 20,10,5,25.Összegezve
|
SOR |
OSZLOP |
ADAT |
|
1 |
1 |
20 |
|
1 |
2 |
10 |
|
2 |
1 |
5 |
|
2 |
2 |
25 |
Ezután
A DATA/Weight Cases opciót kiválasztva beállítjuk az ADAT változót, mint súly.
WEIGHT
BY adat .
Statistics/Summarize/Crosstabs…
CROSSTABS
/TABLES=sor BY oszlop
/FORMAT= AVALUE NOINDEX BOX LABELS TABLES
/STATISTIC=CHISQ
/CELLS= COUNT .
A próba neve: c 2, értéke 15.42857
Nullhipotézis: A sport aktivitás függetlennek tekinthetö a nemektőll
Alternatív hipotézis: A sport aktivitás függ a nemektől
szabadságfok (df): 1
p-érték: 0.00009
Értelmezés A p érték alapján (p<0.05) a nullhipotézist elvetjük, a sport aktivitás függ a nemektől.
.
SPSS output:
SOR by OSZLOP
OSZLOP Page 1 of 1
Count |
|
| Row
| 1.00| 2.00| Total
SOR --------+--------+--------+
1.00 | 20 | 10 | 30
| | | 50.0
+--------+--------+
2.00 | 5 | 25 | 30
| | | 50.0
+--------+--------+
Column 25 35 60
Total 41.7 58.3 100.0
Chi-Square Value DF Significance
-------------------- ----------- ---- ------------
Pearson 15.42857 1 .00009
Continuity Correction 13.44000 1 .00025
Likelihood Ratio 16.27867 1 .00005
Linear-by-Linear 15.17143 1 .00010
Association
Fisher's Exact Test:
One-Tail .00009
Two-Tail .00010
Minimum Expected Frequency - 12.500
Minta 3. Tekinthető-e szabályosnak az a játékkocka, amelyet 1200-szor feldobva, az egyes számok gyakoriságára az alábbi eloszlást kapjuk:
1-es: 195 , 2-es : 210 , 3-as: 190 , 4-es : 204 , 5-ös: 205 , 6-os : 196
Megoldás:
Mivel a kockadobásnál az 1-6-ig a valószínűségek azonosak (p=0.1666), ezért azt várnánk, hogy mind a 6 eset azonos számban, 200-szor forduljon elő
NPAR TEST
/CHISQUARE=dobas
/EXPECTED=EQUAL
/MISSING ANALYSIS.
Null hipotézis:A gyakoriságok megoszlása egyenletes, megfelel a várakozásnak
Alternatív hipotézis: A gyakoriságok megoszlása eltér a várt értékektől
Mit állapíthatunk meg a teszt alapján?
E1. Ugyanebben a file-ban vizsgáljuk meg, hogy a fiúk és lányok egyformán találták-e nehéznek a biometriát!
Mi a nullhipotézis
Eredmények:
Gyakoriságok (kontingencia táblázat)
c 2
szabadságfok (df)
p-érték
Várt gyakoriságokra vonatkozó feltétel teljesül-e
Fisher próba eredménye
Értelmezés
E2. Vizsgáljuk a nemek és az örül (örül-e, hogy megismerhet egy jó kis statisztikai rendszert) kérdésre adott válaszok közötti összefüggést!
Mi a nullhipotézis?.........
Adjuk meg a gyakorisági táblázatot, és az értékelést (Minek alapján döntött).
E3.
Olvassuk be a KISKERD.SAV adatfile-t. Van-e összefüggés a nem és a hobby (pl. zene vagy tánc).Vizsgáljuk a nemek és a zenekedvelés (táncolás) összefüggését! A sejtés az, hogy a két dolog összefügg egymással ( ez az alternatív hipotézis).Nullhipotézis: a zenekedvelés (táncolás) független a nemtõl (azonos arányban szeretik a zenét a fiúk és lányok).Legyen a =0.05 (azaz a szint=95%).
E4. Készítsünk gyakorisági táblázatot a KERD94 file NEM és UDITO nevű változója alapján. Végezzük el a chi-négyzet próbát. Milyen következtetést von le az eredmény alapján 95%-os szinten? Mi itt a nullhipotézis?
E5. A hajszín és egy speciális mérgező anyagra való érzékenységet vizsgálta egy kutató. 300 önkéntest vizsgált meg és a következő eredményeket kapta.
Vörös Szőke Barna Fekete
Kiütést kapott 10 30 60 80
Nem kapott 20 30 30 40
Teszteljük a hipotézist 99%-os szinten! ...........
E6. Vizsgáljuk a KERD94 file-ban a nemek és a szükséges kérdésre adott válaszok közötti összefüggést, azaz, hogy a szükséges-e a biostatisztika kérdésre adott válaszok függetlenek-e a nemtől! (Nem: 1-fiú 2-lány, szükséges-e a biostatisztika, 1-igen 2-nem). Adjuk meg a gyakorisági táblázatot és az értékelést. A fiúk vagy a lányok tartották-e inkább szükségesnek a biostatisztikát? Szignifikáns-e a különbség ? Indokoljuk a döntést.
E7. Vizsgáljuk meg a KERD98.SAV file-ban az ENNI(mennyire szeret enni) változó és a NEM változó kapcsolatát. A fiúk vagy a lányok szeretnek-e jobban enni?
E8. Egy kísérlet során kiderült, hogy két egyetemi csoportban a fiúk közül 7-en dohányoznak, 8-an nem. A lányok közül 28 a dohányos és 7 nem az. Hogyan tudnánk ezekből az adatokból eldönteni, hogy az egyetemisták esetében a fiúk vagy a lányok között magasabb a dohányzók aránya? (95%-os szinten). Mi itt a nullhipotézis ? (Forrás: Hajtman Béla)
E9. Az egyetemi előadások elnéptelenedésének egyik szomorú megfigyelője úgy látta, hogy a fiúk kevésbé járnak órákra, mint a lányok. 30 fiúból mindössze 10 járt rendszeresen előadásokra, míg 90 lány közül éppen a fele. Alátámasztják ezek az adatok a lányok szorgalmasabb óralátogatását? (alfa=0.05) Mi itt a nullhipotézis? (Forrás: Hajtman Béla)
12. Boldogít-e a pénz? ? 20 magas és 40 alacsony jövedelműt vizsgáltak meg, hogy elégedettek-e. A vizsgálat a magas jövedelműek felét, az alacsony jövedelműek 3/4-ét mutatta kiegyensúlyozottnak. Állapítsuk meg a megfelelő próbával, hogy van-e különbség a két csoport között 95%-os szinten. (Forrás: Hajtman Béla)
E10. Gyermekgyógyász szívspecialisták foglalkoztak azzal a kérdéssel, hogy a veleszületett rendellenességek összefüggésben vannak-e az anyát a terhesség első 3 hónapjában sújtó megbetegedésekkel. Az összes vizsgált, rendellenességgel született gyereknél és a véletlenszerűen választott 100 fős kontrollcsoportban a következő volt az eredmény:
Rendellenességgel született 210 újszülöttnél 26 esetben volt az anya beteg és 184 esetben nem, míg a 100 nem rendellenességgel született újszülöttnél 5 esetben volt az anya beteg és 95 esetben nem.
Döntsük el: Függetlennek tekinthető-e az anyáknál történő megbetegedés a gyermekek veleszületett rendellenességétől.
Mit állapíthatunk meg a teszt alapján?
II/2.F. Vegyes gyakorló feladatok
A feladatokat az SPSS program segítségével oldja meg és az output eredmények alapján (a megfelelő számértékek megadásával) a jelen feladatlapon írásban válaszoljon. A szöveges választ kívánó kérdésekre tömören, 1-1 kerek mondatban fogalmazva válaszoljon!
1. a) Nyissa meg a DG981A.SAV adatfile-t, amely egy betegség súlyossági fokára (STATUSZ) és a vérnyomásra (VERNYOM) vonatkozó adatokat tartalmaz. Adja meg a változók adattípusát a megfelelő alternatíva aláhúzásával:
STATUSZ: diszkrét_folytonos, kvalitatív_kvantitatív, nominális_ordinális
VERNYOM: diszkrét_folytonos, kvalitatív_kvantitatív, nominális_ordinális
b) Ábrázolja a STATUSZ változó gyakorisági megoszlását!
Felhasznált SPSS-eljárás:
Enyhe kategória gyakorisága:
relatív gyakoriság:
c) Számítsa ki a vérnyomás átlagát és szórását betegcsoportonként.
Enyhe csoport (STATUSZ=1): n=___ átlag=___________ szórás=___________
Közepes csoport(STATUSZ=2): n=___ átlag=___________ szórás=___________
Súlyos csoport (STATUSZ=3): n=___ átlag=___________ szórás=___________
d) Az átlagok alapján lát-e jelentősebb összefüggést a betegség súlyossági foka és a vérnyomás nagysága közt (ha igen, miért, ha nem, miért nem)?
2. a) Számítson 99%-os konfidenciaintervallumot a vérnyomásra!
Alsó határ (a):
Felső határ (b):
b) Végezzen próbát a
=0.05 hibaszinten azon nullhipotézis ellenőrzésére, hogy a populáció vérnyomás-átlaga egyenlő 120-szal!
Alkalmazott eljárás:
Próba elméleti feltétele:
Döntés (indoklással):
c) A próbához kapcsolódó mintajellemzők értékei:
3. a) Nyissa meg az DG981B.SAVadatfile-t, amely egy kezeléshez használt szer típusára (SZER) és a systolés vérnyomásra (SYSTOLE) vonatkozó adatokat tartalmaz. Adja meg a változók adattípusát a megfelelő alternatíva aláhúzásával:
SZER: diszkrét_folytonos, kvalitatív_kvantitatív, nominális_ordinális
SYSTOLE: diszkrét_folytonos, kvalitatív_kvantitatív, nominális_ordinális
b) Ábrázolja a SZER változó gyakorisági megoszlását!
Felhasznált SPSS-eljárás:
'B' szer kategória gyakorisága:
relatív gyakoriság:
c) Számítsa ki a vérnyomás átlagát és szórását kezelési típusonként.
Placebo (SZER=0): n=___ átlag=___________ szórás=___________
'A' szer (SZER=1): n=___ átlag=___________ szórás=___________
'B' szer (SZER=2): n=___ átlag=___________ szórás=___________
d) Az átlagok alapján lát-e jelentősebb összefüggést a kezelés típusa és a systolés vérnyomás nagysága közt (ha igen, miért, ha nem, miért nem)?
4. a) Számítson 95%-os konfidenciaintervallumot a systolés vérnyomásra!
Alsó határ (a):
Felső határ (b):
b) Végezzen próbát a
=0.01 hibaszinten azon nullhipotézis ellenőrzésére, hogy a systolés vérnyomás várható értéke egyenlő 110-zel!
Alkalmazott eljárás:
Próba elméleti feltétele:
Döntés (indoklással):
c) A próbához kapcsolódó mintajellemzők értékei:
5. Mentse el az output ablak tartalmát (számítási eredmények) az A:\ könyvtárba a saját login nevén (.SPO kiterjesztéssel).
A következő feladatok megoldásához nyissa meg a
DOLG982.SAV SPSS-adatbázisfile-t! A feladatok szövege alapján válassza ki és futtassa le a megfelelő statisztikai eljárásokat és az output eredmények alapján (a megfelelő számértékek megadásával) tömören, 1-1 kerek mondatban válaszoljon minden feltett kérdésre ill. indokolja az eredményeket. 6. Háromféle kezelésnek a diastolés vérnyomásra gyakorolt hatását kell összehasonlítani. Az egyes páciensek vérnyomás-adatát a DIASTOLE változó, az alkalmazott kezelés fajtáját -- 1,2,3 kódokkal -- a KEZELES változó tartalmazza. Mi az alkalmazandó SPSS-eljárás angol neve és a módszer magyar megnevezése?
a) Az összehasonlítás szempotjából lényeges/érdekes mintajellemzők értékei
b) Kimutatható-e lényeges különbség a kezelések hatásában? Mi alapján döntött? Milyen statisztikai próbán alapul a döntés és mi a próba nullhipotézise?
c) Ha a b) pontban szignifikáns különbséget talált, akkor azt is vizsgálja meg az SPSS-eljárás segítségével, hogy melyik két kezelés hatásában van különbség? Milyen statisztikai módszeren / próbán alapszik az eredmény?
7. Egy betegcsoportban azt vizsgáljuk, hogy a systolés vérnyomásnak (SYSTOLE változó) az életkor (KOR változó) növekedésével kimutatható-e egy szignifikáns lineáris trend (tendencia) ill., hogy milyen erős ez a statisztikus kapcsolat. Mi az alkalmazandó SPSS-eljárás angol neve és a módszer magyar megnevezése?
a) Adja meg a lineáris kapcsolatot leíró egyenletet y=a+bx formában, ahol a, b helyére a módszer által számolt becsült paraméter-értékeket írja.
b) Milyen mérőszámmal mérjük a lineáris kapcsolat erősségét és itt mennyi az értéke? Szignifikáns-e a lineáris kapcsolat (indoklás)? Milyen próbán alapszik a döntése és mi a nullhipotézis? (7 p)
c) A becsült a,b paraméterek szignifikánsak-e (miért igen, miért nem)? Milyen próbán alapszik a döntése és mi a nullhipotézis?
8. Betegek és egészségesek láz-értékeit (LAZ változó) kell összehasonlítanunk. A BETEG változó kódolása: 1:egészséges, 2:beteg. Mi az alkalmazandó SPSS-eljárás angol neve és a módszer magyar megnevezése?
a) Az összehasonlítás szempotjából lényeges/érdekes mintajellemzők értékei:
b) Kimutatható-e lényeges különbség a láz-átlagok között? Mi alapján döntött? Milyen statisztikai próbán alapul a döntés és mi a próba nullhipotézise?
c) A normális eloszlás feltételén kívül még minek kell teljesülnie a módszer alkalmazhatóságához? Az alkalmazott SPSS-eljárás (megfelelő részeredménye) alátámasztja-e ezt a további feltételt? Mi alapján döntött a feltétel teljesüléséről (milyen statisztikai próba, annak mi a nullhipotézise)?
9. Egy betegség meglétének a nemmel való kapcsolatát (összefüggését vagy függetlenségét) kell megvizsgálni. Ehhez a mintaadatok: a BETEG változó kódolása: 1="egészséges", 2="beteg", továbbá a NEM változó kódolása: 1="férfi", 2="nő". Mi az alkalmazandó SPSS-eljárás angol neve és a módszer magyar megnevezése?
a) Adja meg az adatokat tömören reprezentáló táblázatot! Mi ennek a neve a biostatisztikában?
b) Független-e a betegség jelenléte a nemtől? Mire alapozza döntését?. Mi az alkalmazott statisztikai próba és annak mi a nullhipotézise a jelen vizsgálatra alkalmazva?
c) Milyen a vátozók adattípusa? Milyen mérőszámokkal jellemezhető a kapcsolat erőssége (adjon meg legalább kettőt) és azoknak mi lett a számított értéke?
10. Mentse el az output ablakot a saját rövid login neve alatt (.SPO kiterjesztéssel az A: meghajtó gyökérkönyvtárába (A:\loginnev.SPO).
11 Vizsgáljuk meg 0.01 szignifikancia szinten, hogy az egyetemi hallgatók vércsoport megoszlása azonos-e a vérbank által az össz lakosságra vonatkózó adatokkal (0: 0.44; A: 0.41; B: 0.10; AB: 0.05). A vizsgált csoportban (120 fő) 0: 54; A: 52; B: 8 és AB: 6.
Mit állapíthatunk meg a teszt alapján?
12. Hallgatókat vallásuk és politikai nézeteik szerint csoportokba soroltuk. Állapítsuk meg, hogy vajon függ a politikai nézet a vallástól?
Demokraták (200 fő):30 buddhista, 30 zsidó, 40 protestáns, 60 római katolikus és 40 egyéb
Republikánusok (100 fő):10 buddhista, 10 zsidó, 40 protestáns, 20 római katolikus és 20 egyéb
Függetlenek (100 fő):10 buddhista, 10 zsidó, 20 protestáns, 20 római katolikus és 40 egyéb
Mit állapíthatunk meg a teszt alapján?
13. A 80-as és 90-es évek egyetemi hallgatóit a következő kérdés alapján próbálják összehasonlítani: Fogyasztźe rendszeresen alkoholt? A 80-as évek diákjaiból 100-ból 62 igennel a többi nemmel válaszolt, míg másik csoportban 120 főből 86 válaszolt igennel. Állapítsuk meg 0.05 szinten , hogy vanźe különbség a két generáció között?
Mit állapíthatunk meg a teszt alapján?
14. Kutatók vizsgálták az összefüggést a "tölgyfa-pollenózis" és a hajszín között. 300 önkéntest vizsgáltak meg és a következő megoszlást találták:
Kiütéses tünet volt: 10 vörös hajúnál, 30 szőkénél, 60 barnánál és 80 feketénél
Kiütéses tünet nem volt: 20 vörös hajúnál, 30 szőkénél, 30 barnánál és 40 feketénél.
Kérdés a hajszín hajlamosítźe a tölgyfa allergiára?
Mit állapíthatunk meg a teszt alapján?
15. Egy baleseti sebészeti ambulancián 10 héten keresztül figyelték a naponkénti balesetek számát. Az adatok a következők:
hétfő: 22, kedd: 21, szerda 23, csütörtök 25, péntek 21 , szombat 46 és vasárnap 17 fő. Vajon azonos forgalom van a hét napjain a baleseti ambulancián?
Mit állapíthatunk meg a teszt alapján?
Különbözik a hétvégi forgalom a hétköznapitól?
A következő feladatokhoz az adatok a DOGA.SAV file-ban találhatók.
16. Összefügg a dohányzási (DOHANY) szokás az iskolázottsággal (ISKOLA)? (DOHANY=1 dohányzik DOHANY=2 nem dohányzik)
Melyik próba használható?
Készítsen táblázatot az adatok megoszlásáról!
17. Készítsen oszlop diagrammot a nemenkénti (NEM) magasság (MAGASSAG) eloszlásáról! Mentse el a floppy-ra LOGINNÉV.CHT néven! (környezeti azonosító nélkül !)
18. Készítsen konfidencia intervallumot az magassag (MAGASSAG) változó adatain! Mentse el a floppy-ra LOGINNÉV.CHT néven! (környezeti azonosító nélkül)!
19. Hasonlítsd össze a magasság (MAGASSAG) és ideális magasság (IDEALMAG) változók átlagát oszlopdiagram segítségével! Mentsd el a floppy-ra az ábrát LOGINNÉV.CHT néven! (környezeti azonosító nélkül ) !Az adatok a KERD98.SAV file-ban található!
20. Egy dohányzás elleni reklám film hatékonyságát szeretnénk tesztelni 10 önkéntes részvételével. A heti átlagos cigaretta fogyasztást (doboz/hét) a film megtekintése előtt a BEFORE változó, a film megtekintése után az AFTER változó tartalmazza. A file a SMOKERS.SAV néven van elmentve!
Hatásos-e a film 95%-os szinten?Mi alapján döntünk?
21. Egy dohányzás elleni reklám film hatékonyságát szeretnénk tesztelni 10 önkéntes részvételével. A heti átlagos cigaretta fogyasztást (doboz/hét) a film megtekintése előtt a BEFORE változó, a film megtekintése után az AFTER változó tartalmazza. A file SMOKERS.SAV néven van elmentve!
Hatékonynak tekintjük a filmet ha a film megtekintése után az átlagos heti cigaretta fogyasztás legfeljebb 2 doboz.
Hatásos-e a film 95%-os szinten?Mi alapján döntünk?
22. Eltér-e a csoport átlagos testmagassága (MAGASSAG) 170 cm-től 95%-os szinten Az adatok a DOGA.SAV file-ban találhatók.
Melyik próba használható?
Jellemezze a MAGASSAG változót! Döntését indokolja!
23. Eltér-e a testmagasság a 171.9 cm-től. Vizsgáljuk a kérdést 95%-os szinten a KERD98.SAV magassag adatain!
Mi alapján döntünk. Jellemezd a MAGASSAG változót! Rajzolj konfidencia intervallumot a MAGASSAG változóra!
24. Ki akarjuk mutatni, hogy egy kezelés, amelyet ugyanazon embereken végeztek, hatást gyakorol a vérnyomáscsökkenésre . Az alábbi értékeket kaptuk:
Kezelés előtt: 190 180 23
0 220 200Kezelés után: 120 140 140 150 150
Mit állapíthatunk meg a teszt alapján 95%-os szinten?
25. Ki akarjuk mutatni, hogy egy kezelés, amelyet állatokon végeztek, hatást gyakorol a testsúlynövekedésre. A testsúly értéket dekagrammban mérve az alábbi adatokat kaptuk:
Kezelés előtt (ELOTT): 53 59 63 67 60 57 73 65 58 68 62 71
Kezelés után (UTAN): 61 52 47 51 58 64 60 55 49 53 60 68
Hatásos-e a kezelés 95%-os szinten?
Mi alapján döntünk. Jellemezze a változókat!
26. Eltér-e a csoport átlagos testmagassága (MAGASSAG) 170 cm-től 95%-os szinten Az adatok a DOGA.SAV file-ban találhatók.
Melyik próba használható?
Jellemezze a MAGASSAG változót! Döntését indokolja!
27.Befolyásolja a dohányzás(DOHANY) a testsúlyt (SULY)? Az adatok a DOGA.SAV file-ban találhatók. (DOHANY=1 dohányzik DOHANY=2 nem dohányzik)
Jellemezze a SULY változót csoportok szerint! Döntését indokolja!
Melyik próba használható?
28.) Rajzoljuk meg a TESZT2 file-beli MAGASSAG és TESTSULY közti lineáris összefüggést kifejező regressziós egyenest!
Hány kilogrammos testsúly tartozna ideális esetben a 175 cm-es magassághoz?
29. Készítsen konfidencia intervallumot a KERD98.SAV file magassag (MAGASSAG) változó adatain! Mentse el a floppy-ra LOGINNÉV.CHT néven! (környezeti azonosító nélkül )!
30. Hasonlítsa össze Bonferoni módszerével a különböző iskolai végzettségű (ISKOLA) emberek testsúlyát(SULY). Az adatok a DOGA.SAV file-ban találhatók.
Jellemezze a SULY változót csoportok szerint!
31. Befolyásolja a testmagasság(MAGASSAG) a testsúlyt (SULY)? Adja meg és jellemezze a lineáris modellt! Az adatok a DOGA.SAV file-ban találhatók.
32. Eltér-e a csoport átlagos testmagassága (MAGASSAG) 176 cm-től 95%-os szinten Az adatok a DOGA.SAV file-ban találhatók. Melyik próba használható?
Jellemezze a MAGASSAG változót! Döntését indokolja!
33. Eltér-e a csoport átlagos testsúly (SULY) 65 kg-tól 95%-os szinten Az adatok a DOGA.SAV file-ban találhatók. Melyik próba használható?
Jellemezze a SULY változót! Döntését indokolja!
34. Befolyásolja a dohányzás(DOHANY) a testmagassagot (MAGASSAG)? Az adatok a DOGA.SAV file-ban találhatók. (DOHANY=1 dohányzik DOHANY=2 nem dohányzik)
Jellemezze a MAGASSAG változót csoportok szerint! Döntését indokolja!
Melyik próba használható?
35. Hasonlítsa össze Bonferoni módszerével a különböző fogamzásgátló módszereket használó emberek (VEDMOD) testsúlyát (SULY). Az adatok a DOGA.SAV file-ban találhatók.
Jellemezze a SULY változót csoportok szerint! Döntését indokolja!
Melyik próba használható?
36. Cummins 1983-ban a heti nátrium fogyasztás és a keringési betegségek közti összefüggést vizsgálta. Adatai a következők:
Év Konyhasó Kenyér Egyéb Keringési betegségben
elhalálozott férfiak/100 000/
'58 10.8 7.2 26.5 673
'59 10.8 7.2 26.4 667
'60 10.0 7.0 25.6 671
'61 9.2 6.90 24.8 662
'62 9.4 6.7 25.0 672
'63 9.9 6.6 25.3 670
'64 10.4 6.4 25.6 670
'65 9.6 6.2 24.7 645
'66 9.6 5.9 24.3 629
'67 9.7 6.1 24.9 595
'68 10.6 5.9 25.4 597
'69 10.1 5.8 24.9 588
'70 11.0 5.8 26.0 573
'71 10.1 5.5 24.5 564
'72 10.8 5.3 24.8 569
'73 9.4 5.1 23.2 547
'74 11.9 5.1 25.6 532
'75 8.1 5.2 21.9 511
'76 8.1 5.1 21.8 494
'77 9.4 5.0 23.0 475
'78 9.6 4.9 22.1 476
Milyen tendenciát láthatunk az évek során a keringési betegségek okozta halálozásoknál? Milyen mortalitási érték várható 1994-ben?
Vizsgáljuk meg, hogy melyik nátrium forrás befolyásolja legjobban a mortalitást!
37. Lehet-e lineáris kapcsolat a testmagasság(MAGASSAG) a testsúly (SULY) között? Definiálja és jellemezze a lineáris modellt! Mekkora magasság tartozik 75 kg-os testsúlyhoz?
Az adatok a DOGA.SAV file-ban találhatók.
38. 25 túlsúlyos férfit három különböző módszerrel próbálnak lefogyasztani: diétával, mozgással vagy étkezési szokás módosításával. A súly változást két hónap után rögzítették. Az eredmények a következők:
Diétás csoport: 1 2 -1 -2 5 10 3 0 2
Mozgás terápiás csoport: -1 6 4 2 2 -3 4
Étkezési szokás módosított csoport: 5 4 1 2 11 -2 4 6 5
A negatív érték súlygyarapodást jelent!
Hasonlítsuk össze a módszereket! Mit állapíthatunk meg?
Mit állapíthatunk meg a teszt alapján?
39. Összefügg a dohányzási (DOHANY) szokás a használt fogamzásgátló módszerrel (VEDMOD)? (DOHANY=1 dohányzik DOHANY=2 nem dohányzik) Az adatok a DOGA.SAV file-ban találhatók.
Melyik próba használható? Készítsen táblázatot az adatok megoszlásáról! Döntését indokolja!
40. Olvassuk be a LANYOK.SAV adatafile-t. Az adatok egészséges középiskolás tanulólányok adatait tartalmazzák egy kérdőíves vizsgálat után.A tanulólányok étkezési szokásait, szociális helyzetét és deviáns magatartását, valamint ezek kapcsolatát vizsgálták. Ebben a file-ban a sok változó közül a következő változókat fogjuk vizsgálni:
|
AZON |
Azonosító szám |
|
. . . |
|
|
SZOM |
Volt-e levert időszaka életében : 1=igen, 2= nem , 9= nincs adat, hiányzó értéknek van kódolva, a számításoknál nem lesz figyelembe véve |
|
ONGY |
Öngyilkossági késztetés 1: sohasem volt, 2: foglalkoztam a gondolatával |
|
ALK |
Alkoholfogyasztás 2 társaságban iszom 3 rendszeresen iszom |
|
. . . |
|
|
JSULY |
Jelenlegi testsúlya |
|
KSULY |
Kívánatos testsúlya |
|
MAGAS |
Testmagasság |
|
ENNI |
Mennyire szeret enni 2 meglehetősen 3 közömbös 4 alig 5 egyáltalán nem 9 nincs válasz |
|
EVES |
Szeret-e enni , 1= igen 2=nem |
|
... |
|
|
EAT4 |
Rettegek, hogy elhízom (Milyen gyakran jut eszébe?) |
40a. Vizsgáljuk meg, hogy függ-e az öngyilkossági hajlam attól, hogy volt-e már szomorú időszaka az életének. Azaz, egyenlő-e az öngyilkosok aránya abban a csoportban, akik még nem voltak szomorúak, illetve, akik már igen. Adjuk meg a gyakorisági táblázatot, a próba feltételeit és a próba eredményét. Melyik csoport foglalkozott inkább az öngyilkosság gondolatával, azaz melyik csoportban nagyobb az öngyilkossági kísérlet relatív gyakorisága?
40b. Vizsgáljuk meg, hogy függ-e az alkoholfogyasztás attól, hogy volt-e már szomorú időszaka az életének. Azaz, egyenlő-e az alkoholfogyasztók és nem fogyasztók aránya abban a csoportban, akik még nem voltak szomorúak, illetve, akik már igen. Adjuk meg a gyakorisági táblázatot, a próba feltételeit és a próba eredményét.
Melyik csoport iszik inkább, a szomorúak, vagy a nem szomorúak? (azaz melyik csoportban nagyobb a “rendszeresen iszom” válasz relatív gyakorisága?
41c.Vizsgáljuk meg, hogy függ-e az öngyilkossági késztetés attól , hogy fogyaszt-e alkoholt. Adjuk meg a gyakorisági táblázatot, a próba feltételeit és a próba eredményét. Melyik csoport foglalkozott inkább az öngyilkosság gondolatával, azaz melyik csoportban nagyobb az öngyilkossági kísérlet relatív gyakorisága?