Veszteséges kódolás introkban
Flag'98 Coder-l elôadás
rod/mandula[s5001pap@hszk.bme.hu]
- Bevezetés
- kódolások csoportosítása
- színmodell választás
- transzformációs kódolás (DCT)
- kvantálás
- a kódolás befejezô lépései
- számítási komplexitás
- kódolási hibák
- introk veszteséges kódolással
- Kódolások csoportosítása
- veszteséges, veszteségmentes
- pixelalapú, blokkalapú
- Színmodell választás
Ebben a leírásban a képek veszteséges tömörítésérôl olvashatsz. Csak olyan képekkel foglalkozunk, ahol a pixelek színkomponensenként vannak tárolva, nem pedig palettából indexelve.
A tárgyalt algoritmus a JPEG és MPEG kódolásának is alapja.
A színmélység lehet bármilyen, ez nem befolyásolja az algoritmust, de kisebb mélységgel jobb tömörítés érhetô el, mert a komponensegyütthatók jobban kvantálhatóak. Pl. egy 24 bites kép esetén a pixelek komponensei 8 bitet foglalnak el, míg egy 15 bites képnél csak 5-öt. Természetesen az eljárás használható grayscale képek kódolására is. Ilyenkor csak egy komponenst kódolunk a szokásos háromhoz képest.
Amikrôl szó lesz:
Veszteségmentes tömörítéssel kb. 1.5-2-szeres tömörítés érhetô el, ez az arány veszteségessel sokkal nagyobb, hátránya, hogy a kódolás után kitömörített kép nem lesz azonos az eredetileg kódolttal.
A pixelalapú kódolás egy ütemben egy pixelt kódol, míg a blokkalapú egy tipikusan 8x8-as blokkot, amivel nagyobb nyereséget kapunk.
A következôkben a veszteséges, blokkalapú kódolást tárgyaljuk meg.
A képek kódolásában jelentôs szerepet játszik, hogy milyen modellt választunk a kép leírására.
A látható színek nagy része elôállítható az r,g,b komponensek additív keverésével, de ez nem hatékony, mert a komponensek átviteléhez nagyjából ugyanakkora sávszélesség szükséges, azaz a komponensek tárolására közel ugyanannyi bitet kell használnunk. Egy kicsit megdobhatja a tömörítést, hogy a zöld komponens a legfontosabb, valamint a szemünk a kék színre a legkevésbé érzékeny. De ennél van sokkal jobb megoldás is.
Képünket világosság és színkülönbségi jelek alapján fogjuk tárolni az YUV rendszerben. RGB modellbôl konvertálás a következô képletek alapján történhet:
y=0.3r+0.59g+0.11b a színjel világossága, fénysûrûség u=(b-y)/2.03 kék színkülönbségi jel v=(r-y)/1.14 vörös színkülönbségi jelvagy mátrixos formában:
|y| | 0.299 0.587 0.114 | |r|
|u| = | -0.147 -0.289 0.437 | |g|
|v| | 0.615 -0.515 -0.100 | |b|
|r| | 1 0 1.140 | |y|
|g| = | 1 -0.394 -0.581 | |u|
|b| | 1 2.028 0 | |v|
Az YUV modellben az u,v komponenseknek nincs fényességtartalmuk, csak az adott jel színérôl hordoznak információt. Elônye a felbontásnak, hogy az emberi szem számára az u,v felbontóképesség 4-5-ször kisebb, mint az y-é. Ezt kihasználva az RGB képünket YUV modellbe konvertálva, tömörítve, az u,v mintákat sokkal jobban kvantálva nagyobb tömörítést érhetünk el, mint RGB kép esetén. Kitömörítéskor pedig a kapott y,u,v értékeket visszaszámoljuk r,g,b-re.
A traszformációs kódolás alapelve, hogy a képet NxN-es blokkokra osztjuk és a frekvenciasíkra transzformáljuk, aminek eredménye NxN együttható lesz. Ez azért kedvezô számunkra, mert az eredeti kép minden pixele azonosan fontos volt, a transzformáltnál viszont az energiatartalom csak bizonyos együtthatókba tömörül, a többi amplitúdója kicsi. Tipikusan az NxN-es blokk transzformációjakor kapott értékek elsô elemei nagyobb információt hordoznak mint a nagyobb indexûek, ezért a kvantáláskor ennek megfelelô bitszámot állapítunk meg nekik.
A hátsó együtthatók nagy része el is hagyható. A tömörítés mértékét az határozza meg, hogy az együtthatókat milyen potossággal ábrázoljuk, azaz hány bitre kvantáljuk.
Ki kell választanunk egy transzformációt, amivel mindezt végezzük. Erre legelterjedtebb a Diszkrét Cosinus Transzformáció (DCT). Elônyei közé tartozik, hogy az együtthatók valósak és a számításigény megfelelô. Többek között ezt használja a JPEG és az MPEG is.
Az 1 dimenziós DCT és inverz DCT képletei:
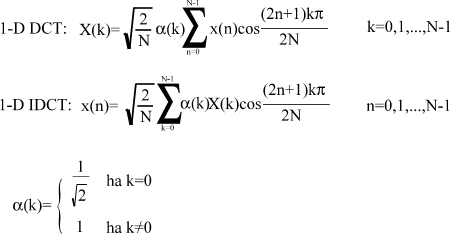
A DCT eredményeként kapott együtthatókat 2 csoportra osztjuk, az X(0)-t DC komponensnek hívjuk és a vektor átlagértékével arányos összetevô. A többi elem (X(k), k>0) pedig AC komponens. Az összes komponens valós.
Mivel mi egy blokkot akarunk kódolni, ami 2 dimenziós, szükségünk lesz egy 2-d DCT-re és inverzére is. Az adott képletekkel analóg módon ez könnyen kihozható. Azért nem írom le, mert felesleges. Ugyanis a DCT szeparálható, azaz a 2-dimenziós felírható 2 darab 1-d transzformáció összegeként úgy, hogy elvégezzük minden sorra és oszlopra az 1-d DCT-t.
példaként itt egy kódrészlet IDCT-re:
void idct2D (double coeffs[8*8], double samples[8*8])
{
int i;
double *sp,*cp;
static double tmp[8*8];
for (sp = tmp, cp = coeffs, i = 0; i < 8; i++, sp += 8, cp += 8)
idct1D (cp, 1, sp, 1);
for (sp = samples, cp = tmp, i = 0; i < 8; i++, sp += 1, cp += 1)
idct1D (cp, 8, sp, 8);
}
void idct1D (double coeffs[], int coeffOffset, double x[], int xOffset)
{
double *cp, *xp;
double dc = 0.70710678*coeffs[0];
int i;
static double C[32] = { /* cos(k*pi/16), (0 <= k <= 31) */
+1.00000000, +0.98078528, +0.92387953, +0.83146961,
+0.70710678, +0.55557023, +0.38268343, +0.19509032,
+0.00000000, -0.19509032, -0.38268343, -0.55557023,
-0.70710678, -0.83146961, -0.92387953, -0.98078528,
-1.00000000, -0.98078528, -0.92387953, -0.83146961,
-0.70710678, -0.55557023, -0.38268343, -0.19509032,
-0.00000000, +0.19509032, +0.38268343, +0.55557023,
+0.70710678, +0.83146961, +0.92387953, +0.98078528,
};
for (i = 8, xp = x; --i >= 0; xp += xOffset)
*xp = dc;
for (i = 1, xp = x; i <= 15; i += 2, xp += xOffset)
{
double sum = 0.0;
int u,j;
for (j = i, u = 7, cp = coeffs + coeffOffset; --u >= 0;
j += i, cp += coeffOffset)
sum += C[j & 0x1F] * *cp;
*xp += sum;
}
for (i = 8, xp = x; --i >= 0; xp += xOffset)
*xp *= 0.5;
}
A transzformáció elvégzése után kaptunk egy rakás valós számot, amit valahogy véges bitértéken tárolni kéne. A bitszámok kiosztását, azaz, hogy melyik együtthatót hány biten tároljuk optimalizálni kellene.
Ez két szempont alapján lehetséges. Vagy a rekonstruált blokk torzítását akarjuk minimalizálni, vagy pedig az emberi szem számára megfelelô képet akarunk létrehozni. Számunkra a második sokkal hasznosabb, mert nekünk az számít, hogy minél jobban nézzen ki a tárolt kép, nem pedig, hogy mennyire hasonlít az eredetire.
Ezt hívják a kvantálási mátrix HVS (Human Visual System) alapján történô tervezésének. Ez alapján a nagyobb indexû együtthatókat nagyobb lépcsôvel kvantáljuk.
Itt felhasználhatjuk a YUV modellben tett kijelentésünket, hogy az y komponens sokkal hangsúlyosabb.
Bemutatjuk a JPEG alap kvantálási tábláit:
JPEG default kvantálási tábla y komponensre
{
16.0, 11.0, 10.0, 16.0, 24.0, 40.0, 51.0, 61.0,
12.0, 12.0, 14.0, 19.0, 26.0, 58.0, 60.0, 55.0,
14.0, 13.0, 16.0, 24.0, 40.0, 57.0, 69.0, 56.0,
14.0, 17.0, 22.0, 29.0, 51.0, 87.0, 80.0, 62.0,
18.0, 22.0, 37.0, 56.0, 68.0, 109.0, 103.0, 77.0,
24.0, 35.0, 55.0, 64.0, 81.0, 104.0, 113.0, 92.0,
49.0, 64.0, 78.0, 87.0, 103.0, 121.0, 120.0, 101.0,
72.0, 92.0, 95.0, 98.0, 112.0, 100.0, 103.0, 99.0
}
JPEG default kvantálási tábla u,v komponensre
{
17, 18, 24, 47, 99, 99, 99, 99,
18, 21, 26, 66, 99, 99, 99, 99,
24, 26, 56, 99, 99, 99, 99, 99,
47, 66, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99,
99, 99, 99, 99, 99, 99, 99, 99
}
A kódolást két külön úton fogjuk végezni, AC,DC komponensekre szeparálva. Kezdjük az AC komponensekkel. A kódolt blokkban az értékesebb együtthatók a bal felsô sarokban fognak csoportosulni, ami a kvantálási mátrixok vizsgálatakor is észrevehetô. Emiatt a kódolt blokkon a bal felsô sarokból indulva cikk-cakkban fogunk elindulni és így tároljuk az elemeket, amelyekbôl párokat képezünk a következô módszer szerint: közvetlenül az elem elôtt lévô nullák száma és az értékes (nem 0) együtthatók alkotnak egy párt.
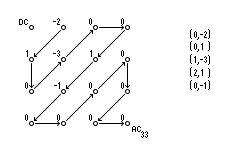
Ezek a run-level párok nagyjából a frekvencia szerint alakulnak ki a cikk-cakk rendezés miatt, ezért több 0 kerül egymás mellé, jóval kevesebb párt kapunk. Bizonyos párok gyakrabban, bizonyosak ritkábban fordulnak elô, ezekhez rendelhetünk változó hosszúságú kódszavakat, pl. Huffman-kódot. A DC együtthatók különbségeit kódoljuk, azaz a DC(i+1)-DC(i) számhoz rendelünk egy Huffman-kódszót.
A Huffman kódolás általában nem optimális Huffman, hanem egy meghatározott táblával kódolnak mindent. A JPEG-ben 2 DC és 2 AC tábla közül lehet választani.
Számítási komplexitás
A számitásigény függ a választott DCT algoritmustól:
| szorzások nagyságrendje | összeadások nagyságrendje | |
| 1-D DCT definíció alapján | N2 | N2 |
| 2-D DCT definíció alapján | N4 | N4 |
| 2-D szeparálással | 2N3 | 2N3 |
A komplexitás a blokkméret függvénye is. Hatékony blokkméret 2 egész számú hatványa. Homogénebb képet kapunk, ha a blokkméretet, minél kisebbre választjuk viszont minél kisebb a blokk, annál több a kisfrekvenciás együttható, finoman kell kvantálni, a tömörítés mértéke kisebb lesz.
4x4-es blokkméretnél nagyon durván kell kvantálni a jó tömörítéshez az elôzôek miatt.
8x8-as blokk az elterjedt, mert jó minôséget ad és jól tömörít.
16x16-os blokkméretnél a tömörítési javulás kis mértékû, viszont a számításigény jelentôsen nô.
A kódolt képeken észrevehetô egy blokkosodási hiba, amikor DCT blokkok határai megjelennek a képen.
Másik probléma a Gibbs-oszcilláció vagy mosquito-zaj, amit az okoz, hogy egy blokkhatáron megy át egy él. Ilyenkor az él körül furcsa elmaszatolódást lehet észrevenni.
A 3 legismertebb veszteséges kódolást használó 64k intro a Black Lotus Jizz és Stash, amik körülbelül 3 mega truecolor képet tartalmaznak, valamint a Pulse Sink nevû introja. A Jizz kimenti a képeket /pandora kapcsolóval a lemezre, a /mp4 opcióval az 1 megás zenét is kiszedhetjük. A Sink titkos opciója a /tgas, sajnos nekem a tga képek hibásak voltak és kimentés után ki is fagyott az intro, ezért pontosan nem tudom, hogy mennyi képet tartalmaz.
A Sink kezdô képén jól észrevehetô mindkét tárgyalt kódolási hiba.

A Jizz ezt úgy védi ki, hogy texturái teljesen elmosottak, valószínûleg 128x128-as képek, amiket átlagolásos módszerrel nagyítottak 256x256-osra és smooth-oltak.

Ez egy vektoreffekt texturájánál alig észrevehetô. Másik alkalmazott trükk pedig az, hogy igaz, hogy a lementett képek 24 bites tga-k, de egy 16 bites introba felesleges ilyen színmélységben tárolni a képeket. Valószínûleg nem kell optimális Huffmant írni a kitömörítôbe, csak letárolni a 2 Huffman táblát AC-re és DC-re. Tovább egyszerüsíthetjük a helyzetünket, ha a tömörítéssel nem foglalkozunk, hanem az exe-tömörítônkre bizzuk pl. pmwlite, wwpack. Bár szerintem így a tömörítési hatásfok csökkenni fog.
Remélem, a leírás segítségével sok magyar intro fog veszteséges tömörítést használni, megnövelve az introk szinvonalát. Ha kérdésetek van, írjatok a s5001pap@hszk.bme.hu, vagy rod@inf.bme.hu címre.