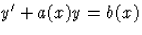Az ${y}^\prime+a(x)y=b(x)$ eset (Ezek az elsőrendű lineáris egyenletek.)  Megemlítjük, hogy az egyenletet azért hívják lineárisnak, mert az ismeretlen y függvény csak az első hatványon szerepel f(x,y)-ban (ami most -a(x)y+b(x)). Az egyenletet az állandó variálásának módszerével oldjuk meg.   Először oldjuk meg a lineáris egyenletünknek megfelelő $${y}^\prime_h+a(x)y_h=0$$ differenciálegyenletet. (Ezt az eredeti, differenciálegyenlethez tartozó homogén egyenletnek, és    megkülönböztetésül az eredeti, nem azonosan 0 jobb oldalú egyenletet inhomogén differenciálegyenletnek nevezik. Vigyázat, nem tévesztendő össze ez a fogalom a változóiban homogén differenciálegyenlet fogalmával!) Erről láthatjuk, hogy szétválasztható változójú, így a megoldás felírása könnyű: ahol A(x) a a(x) függvény egy primitív függvénye és c tetszőleges valós szám. Mivel a jobb oldal mindig pozitív (lévén egy valós szám exponenciális függvénye) és yh folytonos, ezért yh=+ece-A(x), vagy yh=-ece-A(x). Továbbá, az első egyenlethez yh-val való osztással jutottunk, így ellenőrizni kell, vajon yh=0 megoldása-e a (homogén) differenciálegyenletnek. Könnyen láthatjuk, hogy igen. Így a homogén egyenletnek az $$y_h=+e^ce^{-A(x)},\quad\mbox{{az}}\quad y_h=+e^ce^{-A(x)},\quad\mbox{{és az}}\quad y_h=0$$ függvények tesznek eleget. Mivel tetszőleges, ezért ec tetszőleges pozitív szám, így a megoldási képletekben e-A(x) szorzói (rendre ec, -ec, 0) együttesen befutják a valós számok halmazát. Ezért a homogén egyenlet megoldása egy képletben is felírható:   $$y_h=Ce^{-A(x)},\qquad C\in{\rm I\! R}.$$ (40) Mivel nekünk az inhomogén egyenletet kell megoldanunk, ezért próbálkozzunk hasonló alakú függvényekkel: keressük az inhomogén differenciálegyenlet megoldását   y(x)=C(x)e-A(x) (41) alakban, tehát a homogén egyenlet megoldásában szereplő állandót tegyük x-től függővé, , ,variáljuk''. Megjegyezzük, hogy nem zártunk ki egyetlen függvényt sem azzal, hogy az egyenlet megoldását (51) alakjában keressük: tetszőleges y(x) függvényhez van olyan C(x) függvény amellyel y(x)=C(x)e-A(x), ugyanis a C(x)=y(x)eA(x) függvény megfelelő. Helyettesítsük be az (51) alatti y(x) függvényt az eredeti egyenletbe, majd oldjuk meg C(x)-re! (A függvények argumentumában szereplő x-eket a könnyebb olvashatóság kedvéért a második egyenlettől kezdve elhagyjuk.) ahonnan 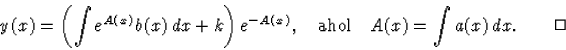$$C(x)=\int{e^{A(x)}b(x)\,dx+k}.$$ (Hogy ne keveredjünk el a sok konstans között, a ${C}^\prime$ integrálása során fellépő integrálási állandót k-val jelöltük.) Ezért a differenciálegyenlet megoldása:   $$y(x)=\left(\int{e^{A(x)}b(x)\,dx+k}\right)e^{-A(x)},\quad\mbox{{ahol}}\quad A(x)=\int{a(x)\,dx}.\qquad\Box$$ (42) Most lássunk néhány kidolgozott feladatot.   4-1. kidolgozott feladat. Oldjuk meg az $${y}^\prime+6y=7$$ differenciálegyenletet! Megoldás: Az egyenlet lineáris. Először oldjuk meg a megfelelő homogén lineáris differenciálegyenletet! $${y}^\prime_h+6y_h=0,\quad\mbox{{innen}}\quad\frac{dy_h}{y_h}=-6dx.\quad\mbox{{integrálva:}}\quad \ln\vert y_h\vert=-6x+c,$$ ezért (figyelembe véve az abszolút érték elhagyásáról a levezetéskor mondottakat) yh=Ce-6x. , ,Variáljuk'' a konstanst, azaz keressük az inhomogén differenciálegyenlet megoldását   y=C(x)e-6x (43) alakban! Visszahelyettesítve ezt az alakot a differenciálegyenletbe kapjuk $${\left(C(x)e^{-6x}\right)}^\prime+6C(x)e^{-6x}=7.$$ Végezzük el a deriválást és egyszerűsítsünk! Ezt megoldva a $$C(x)=\frac76e^{6x}+k,\qquad k\in{\rm I\! R}$$ formulát kapjuk. Beírva a most kapott eredményt (53)-be megkapjuk a differenciálegyenlet megoldását: $$y=\left(\frac76e^{6x}+k\right)e^{-6x}=\frac76+ke^{-6x},\qquad k\in{\rm I\! 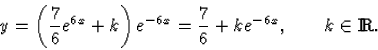R}.$$   4-2. kidolgozott feladat. Adjuk meg az $$\sin(x){y}^\prime+\cos(x)y=1$$ differenciálegyenlet olyan megoldását, amelynek a) $\frac{\displaystyle\pi}{\displaystyle2}$-ben 3, b) 0-ban 1 a határértéke! Megoldás: A megfelelő homogén differenciálegyenletet megoldva Ezért a megoldást az $$y(x)=\frac{C(x)}{\sin(x)}$$ alakban kell keresni. 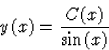Behelyettesítve az inhomogén differenciálegyenletbe kapjuk Ezért a differenciálegyenlet megoldása:   $$y=\frac{x+k}{\sin(x)},\qquad k\in{\rm I\! R}.$$ (44) Az a) kérdést megválaszolandó olyan k számot kell keresni, amelyre $$\lim\limits_{x\to\pi/2}\frac{x+k}{\sin(x)}=3.$$ Mivel $$\lim\limits_{x\to\pi/2}\frac{x+k}{\sin(x)}=\frac{\pi/2+k}{\sin(\pi/2)}= \frac{\pi/2+k}{1}=\frac\pi2+k$$ a számláló és a nevező folytonossága miatt, ezért a)-nak $k=3-\frac{\displaystyle\pi}{\displaystyle2}$ az egyetlen megoldása. 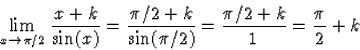A b) kérdés megválaszolásánál óvatosnak kell lennünk, mert 0 nem eleme a (54) alatti y függvények értelmezési tartományának. Azonban 0-nak a bal és a jobb oldali környezetében értelmezve vannak. Próbáljunk olyan k értéket találni, amellyel a fenti y bal és jobb oldali határértéke egyaránt 1. Mivel a nevező határértéke 0, ezért a tört határértéke csak akkor lehet egy véges szám, ha a számlálónak is 0 a határértéke. (De ez nem elégséges hozzá.) Így k csak 0 lehet. Szerencsénkre a k=0-hoz tartozó   $$y=\frac{x}{\sin(x)}$$ (45) függvénynek éppen 1 a határértéke (ezt tudjuk az analízisből), ezért a (55) alatti függvény eleget tesz a kívánalmaknak. Megjegyzés. A (55) alatti y függvény nincs értelmezve 0-ban, de határértéke létezik, ez 1. Így ha értelmezzük y-t a 0 pontban az y(0):=1 egyenlőséggel, akkor folytonos függvényt kapunk. Megmutatható, hogy az így előálló függvény még differenciálható is a 0-ban és ${y}^\prime(0)=0$. Ezért y kielégíti a differenciálegyenletet még ebben a pontban is (hiszen behelyettesítve $x=0,y=1,{y}^\prime=0$-t a differenciálegyenletbe azonosságot kapunk: $\sin(0)\cdot0+\cos(0)\cdot1=1$ valóban).   4-3. kidolgozott feladat. Adjuk meg az $$\left.\begin{array} {rcl} x{y}^\prime+y+x^2 &=&0, \\ y(3)&=&2\end{array}\right\}$$ kezdetiérték-feladat megoldását! 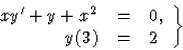Megoldás: Alkalmazzuk most a differenciálegyenlet megoldásának megkeresésére a (52) alatti formulát! Ehhez először a differenciálegyenletet kell a megfelelő alakra hozni. 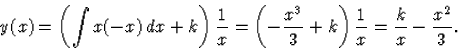$${y}^\prime+\frac1xy=-x,\quad\mbox{{így}}\quad a(x)=\frac1x,\quad b(x)=-x.$$ Ekkor $$A(x)=\int\frac1x\,dx=\ln(x),\quad e^{A(x)}=x,\quad e^{-A(x)}=\frac1x,$$ ezért a differenciálegyenlet megoldása $$y(x)=\left(\int{x(-x)\,dx+k}\right)\frac1x=\left(-\frac{x^3}{3}+k\right) \frac1x=\frac kx-\frac{x^2}{3}.$$ Behelyettesítve a kezdeti értéket $$2=\frac k3-\frac93,\quad\mbox{{ahonnan}}\quad k=15.$$ Tehát a kezdetiérték-feladat megoldása: $$y=\frac{15}{x}-\frac{x^2}{3}.$$   4-4. kidolgozott feladat. Oldjuk meg az $$x{y}^\prime+(2x+1)y=e^{-2x}\sin(x)$$ differenciálegyenletet! Megoldás: A megfelelő homogén egyenletet megoldva A konstanst variálva y-t az $$y=\frac{C(x)}{x}e^{-2x}$$ alakban keressük. Behelyettesítve ezt az inhomogén egyenletbe, majd az előálló differenciálegyenletet C-re megoldva kapjuk így $C=-\cos(x)+k,\quad k\in{\rm I\! R}$.Ezért a differenciálegyenlet megoldása: $$y=\frac{k-\cos(x)}{x}e^{-2x},\qquad k\in{\rm I\! R}.$$   4-5. kidolgozott feladat. Oldjuk meg az $${y}^\prime-\frac 2xy=x\ln(x)$$ differenciálegyenletet! Megoldás: Először adjuk meg a megfelelő homogén egyenlet megoldását! Keressük ezért az inhomogén egyenlet megoldását y=C(x)x2 alakban! Helyettesítsük ezt be a differenciálegyenletbe és oldjuk meg az előálló egyenletet C-re! Ezért a differenciálegyenlet megoldása: $$y=\frac12x^2\ln^2(x)+kx^2.$$

Dr. Horváth Zoltán:Bevezetés a differenciálegyenletek megoldásábaKészült a SZIF-MML-rendszer felhasználásával