![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Az 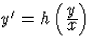 eset
eset
(Ezek a változóiban homogén differenciálegyenletek.)
Ez az eset könnyen visszavezethető egy szétválasztható
változójú differenciálegyenlet megoldására, ha ![]() helyett
bevezetünk egy u új függvényt. Legyen tehát
helyett
bevezetünk egy u új függvényt. Legyen tehát
![]()
![]()
![]()
Ugyancsak szétválasztható változójú differenciálegyenlet megoldására vezet az a feladat, ha a tárgyalt differenciálegyenlet-típusnál valamivel áltolánosabb
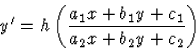
![]()
Joggal merülhet fel a kérdés: a differenciálegyenlet jobb oldalából, f(x,y)-ból hogyan látszik az, hogy az valamilyen h-val h(y/x) alakra hozható? Ezt megválaszolandó vezessük be a homogén függvény fogalmát.
Definíció. Azt mondjuk, hogy az f=f(x,y) függvény
homogén, ha az értelmezési tartományának
minden (x,y) pontjára és minden ![]() valós számra
f(tx,ty)=f(x,y).
valós számra
f(tx,ty)=f(x,y).
Állítás. Az f kétváltozós függvényhez pontosan akkor létezik h egyváltozós függvény, mellyel f(x,y)=h(y/x), ha f homogén.
Bizonyítás. Ha ![]() , akkor minden -ra
, akkor minden -ra
![]()
Másrészt, ha f homogén, akkor egy rögzített x0-lal
![]()
3-1. kidolgozott feladat.
Döntsük el, hogy az alábbi differenciálegyenletek a változóiban
homogénok-e!
1. y^=x^2+y^2xy,
2. y^=x^2-y^2x+y,
Megoldás:
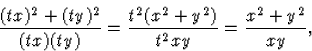
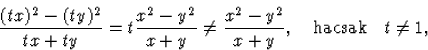
![]()
3-2. kidolgozott feladat.
Oldjuk meg az
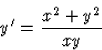
Megoldás:
A differenciálegyenletről már beláttuk, hogy a változóiban homogén (lásd a
(2.3-1.) kidolgozott feladatot). Végezzük el az y=ux
helyettesítést! Mivel ekkor ![]() , ezért a differenciálegyenlet felírható az
, ezért a differenciálegyenlet felírható az
![]()
![]()
Innen, az y=ux összefüggés felhasználásával nyerjük a feladat megoldását az
![]()
3-3. kidolgozott feladat.
Oldjuk meg az
![]()
Megoldás: Fejezzük ki az egyenletből -t!
Látható, hogy az egyenlet jobb oldala ![]() alakú,
így az y=ux helyettesítéssel egy szétválasztható változójú
egyenletet kapunk.
alakú,
így az y=ux helyettesítéssel egy szétválasztható változójú
egyenletet kapunk.
A helyettesítést elvégezve és a változókat szétválasztva:
Integrálva mindkét oldalt:
Fejezzük ki innen u-t!
Ezért az eredeti differenciálegyenlet megoldása:
![]()
3-4. kidolgozott feladat.
Oldjuk meg az
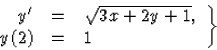
Megoldás: Végezzük el az u=3x+2y+1 helyettesítést, amint azt korábban javasoltuk! Ekkor
![]()
![]()
![]()
![]()
![]()
A differenciálegyenlet jobb oldalán álló integrál kiszámítása egyszerű, így e differenciálegyenlet megoldása:
![]()
![]()
c meghatározásához helyettesítsünk be ebbe az utóbbi képletbe x=2,y=1-et!
![]()
![]()
3-5. kidolgozott feladat.
Oldjuk meg az
![]()
Megoldás:
Helyettesítsük 2x+y-t u-val! Ekkor ![]() , ahonnan
, ahonnan ![]() . Ezért a differenciálegyenlet:
. Ezért a differenciálegyenlet:
![]()
A változókat szétválasztva és integrálva:
![]()
Visszaírva ezt a differenciálegyenletbe kapjuk

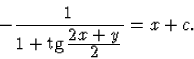
3-6. kidolgozott feladat.
Oldjuk meg az
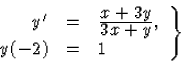
Megoldás: Az egyenlet változóiban homogén, mert
![]()
![]()
![]()
ahonnan a számlálók összehasonlításával az
![]()
Ezt felhasználva (49) az
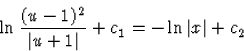
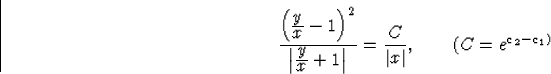
(y-x)2=C|y+x|
adódik.A kezdeti feltételből C-re a 9=C|-1| egyenletet kapjuk, ezért C=9.
Minthogy x+y függvény negatív a kezdeti feltételből, y(-2)=1-ből vett x0=-2,y0=1 pontban, ezért a folytonossága miatt annak egy környezetében is negatív, így itt |x+y|=-(x+y) (mert negatív szám abszolút értéke egyenlő a szám (-1)-szeresével). Ezért a kezdetiérték-feladat megoldásaira az
(y-x)2=-9(y+x)
implicit függvénymegadás érvényes. Ebből explicit alakot is kaphatunk, ha megoldjuk ezt az y-ban másodfokú egyenletet. Figyelembe véve, hogy a megoldás, y pozitív x=-2 közelében azt kapjuk, hogy a kezdetiérték-feladatnak csak az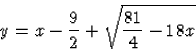
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával