![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Az 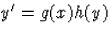 eset
eset
(Ezek a szétválasztható változójú egyenletek.)
Az egyenlet mindkét oldalát h(y)-nal leosztva kapjuk az
| |
(35) |
| |
(36) |
Tehát (45)-ből az alábbi egyenlőség következik:
| H(y(x))=G(x)+c, | (37) |
![]()
![]()
Ezután (46)-ből y(x)-et megpróbálhatjuk kifejezni. Ha nem sikerül, akkor az y megoldást csak a (46) alatti implicit egyenlet tel adhatjuk meg.
Ne feledkezzünk el arról sem, hogy (44)-hez h(y)-nal való osztás útján jutottunk el. Vizsgálni kell még azt az esetet is, amikor az osztó 0 is lehet. Amennyiben a h függvénynek van zérushelye, mondjuk h(y1)=0, úgy az differenciálegyenletnek az y(x)=y1 konstans függvény is megoldása.
Formális számolással egyszerűbben is megkaphatjuk (46)-at.
Most írjuk az derivált helyére a másik, tört alakos
jelölést, ![]() -et, majd ezután a dy és dx
szimbólumokat önállónak tekintve gyűjtsük a bal oldalra az y-t
tartalmazó tagokat, a jobb oldalra az x-et tartalmazókat (ezzel mintegy
, ,szétválasztjuk'' y-t és x-et). Így az
-et, majd ezután a dy és dx
szimbólumokat önállónak tekintve gyűjtsük a bal oldalra az y-t
tartalmazó tagokat, a jobb oldalra az x-et tartalmazókat (ezzel mintegy
, ,szétválasztjuk'' y-t és x-et). Így az
| |
(38) |
egyenlőségeket, ami ugyanaz, mint (46).
Ha ránézünk az egyenletekre, akkor látjuk, hogy a két megoldási mód lényegében lépésről lépésre ugyanaz. A második megoldási mód könnyebben megjegyezhető és ezt is fogjuk használni; az első tulajdonképpen csak a dy és dx szimbólumokkal való számolást legalizálja.
Nézzünk meg most néhány kidolgozott példát.
2-1. kidolgozott feladat.
Oldjuk meg az
![]()
Megoldás: Az egyenlet felírásából látszik, hogy szétválasztható változójú. A megoldást az előbb mondottak szerint végezhetjük. Először szétválasztjuk a változókat:
![]()
y-t kifejezve:
![]()
2-2. kidolgozott feladat.
Oldjuk meg az
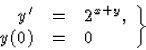
Megoldás:
A differenciálegyenlet jobb oldala szorzattá alakítható, hiszen ![]() .Itt az első tényező csak x-et, a második csak y-t tartalmazza,
ezért a differenciálegyenlet szétválasztható változójú.
.Itt az első tényező csak x-et, a második csak y-t tartalmazza,
ezért a differenciálegyenlet szétválasztható változójú.
Először a differenciálegyenletet oldjuk meg. 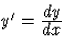 -et beírva
és a változókat szétválasztva kapjuk
-et beírva
és a változókat szétválasztva kapjuk
![]()
Behelyettesítve a kezdeti feltételt:
![]()
![]()
2-3. kidolgozott feladat.
Oldjuk meg az
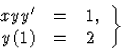
Megoldás: Szétválasztva a változókat, majd integrálva:
![]()
![]()
![]()
![[*]](cross_ref_motif.gif) . oldalt) a megoldás x0 egy környezetében kell, hogy értelmezve legyen.)
. oldalt) a megoldás x0 egy környezetében kell, hogy értelmezve legyen.)
A kezdeti értéket a differenciálegyenlet második megoldásába helyettesítve
![]()
Így a kezdetiérték-feladatnak egy megoldása van, az
![]()
2-4. kidolgozott feladat.
Oldjuk meg az
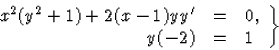
Megoldás: Először fejezzük ki a differenciálegyenletből -t!
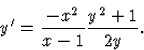
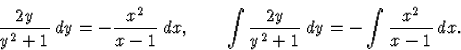
Így y-ra az
![]()
c-t meghatározandó helyettesítsük be a kezdeti feltételből származó x=-2, y=1 értékeket!
![]()
![]()
(Két helyen kellett vigyázni az utolsó egyenlőség felírásánál: a jobb oldalon
álló négyzetgyökjel elé csak a + jel kerülhet, mert a kezdeti feltételben
szereplő y0=1 érték pozitív, így a megoldás is pozitív kell legyen x0
közelében; másrészt |x-1| helyett -(x-1)=1-x írható, hiszen
x0=-2 közelében x-1 negatív.)
2-5. kidolgozott feladat.
Egy kicsi vasgolyót beleteszünk az éppen forrásban lévő vízbe, majd
felmelegedése után kivesszük a ![]() C hőmérsékletű szobába.
1 perc alatt 30
C hőmérsékletű szobába.
1 perc alatt 30![]() C-ot hűlt le.
C-ot hűlt le.
Mennyi idő múlva hűl le újabb 30C-ot?
Megoldás: A vasgolyó hőmérsékletének leírására alkalmazzuk a Newton-féle hűlési törvényt! Így a korábban levezetett (16) egyenlet szerint a vasgolyó T hőmérsékletére a
differenciálegyenletet nyerjük, ahol Tk=20, egyelőre ismeretlen együttható. A feladat szövegéből tudjuk, hogy![]()
Oldjuk meg a differenciálegyenletet! Láthatjuk, hogy az szétválasztható változójú. Először szétválasztva a változókat, majd integrálva:
![]()
Mivel Tk=20 és a kezdeti feltétel T(0)=100, ezért T(0)-Tk>0, ezért a megoldás képletéből az abszolút érték jele elhagyható. Így a megoldás:
| |
(39) |
Határozzuk meg C-t a T(0)=100 kezdeti feltételből! Behelyettesítéssel
![]()
![]()
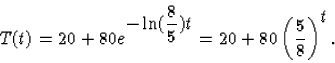
Mivel a differenciálegyenlet megoldásának első lépésében T-Tk-val osztottunk,
ezért meg kell vizsgálni, hogy ![]() megoldása-e a feladatnak!
Láthatjuk, hogy a differenciálegyenletet kielégíti, de a kezdeti feltételt
megoldása-e a feladatnak!
Láthatjuk, hogy a differenciálegyenletet kielégíti, de a kezdeti feltételt ![]() miatt nem, ezért a (48) alatti függvény az egyetlen megoldás.
miatt nem, ezért a (48) alatti függvény az egyetlen megoldás.
Olyan t1 időpontot kell keresnünk, amelyre T(t1)=40. Megoldva a
![]()
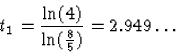
Tehát a vasgolyó közelítőleg 2 perc alatt hűl le újabb
30C-ot.
2-6. kidolgozott feladat.
Milyen geometriai alakzatot alkotnak az
![]()
Megoldás: Fejezzük ki -t az egyenletből!
![]()
Szétválasztva a változókat és integrálva:
![]()
![]()
2-7. kidolgozott feladat.
Egy RC-körben (tehát egy ellenállás és egy kondenzátor
sorbakapcsolásával nyert áramkörben) kikapcsoljuk az áramforrást.
A kikapcsolás utáni pillanatban a rendszerben I0 erősségű
áram folyik.
Határozzuk meg az I áramerősséget a kikapcsolástól mért t idő függvényében!
Megoldás: I-t (13) szerint az
![]()
A differenciálegyenlet szétválasztható változójú, ezért a szokásos módon járhatunk el a megoldásakor.
![]()
![]()
Ebből
![]()
![]()
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával