![[*]](nyil_elore.gif)
![[*]](nyil_vissza.gif)
![[*]](nyil_fel.gif)
![[*]](nyil_tartalom.gif)

Az 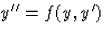 eset
eset
Ez tehát az az eset, amikor a független változó, x nem szerepel a
jobb oldalon. Ez adja az ötletet, hogy próbáljuk y-t tekinteni
független változónak és vele fejezni ki -t és ![]() -t.
-t.
Tudjuk, hogy ha y szigorúan monoton egy intervallumon, akkor itt bármely más függvény felírható az ő függvényeként, így létezik olyan p függvény -höz (y-nak minden egyes szigorú monotonitási intervallumán), hogy
| |
(89) |
| |
(90) |
![]()
| |
(91) |
2-1. kidolgozott feladat.
Oldjuk meg a
peremérték feladatot!
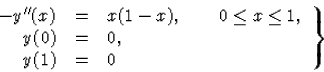
(92)
Megoldás:
Először a differenciálegyenletnek keressük meg az általános megoldását.
Követve a 3.2.1 alfejezetben leírtakat
A peremérték feladat megoldását úgy kapjuk meg, hogy az általános megoldás (108) alatti képletében megválasztjuk a c1 és c2 integrációs állandók értékét az y(0)=0, y(1)=0 feltételeknek megfelelően.
ahonnan
![]()
Tehát a (107) peremérték feladatnak egy megoldása van:
![]()
2-2. kidolgozott feladat.
Oldjuk meg az
kezdetiérték-feladatot!
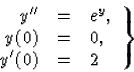
(93)
Megoldás:
A 3.2.3 szakaszban mondottaknak megfelelően szorozzuk be a differenciálegyenlet mindkét
oldalát -vel, majd integráljunk x szerint! Így kapjuk:
22=2e0+c1,
ahonnanc1=0.
Ezért (110) egyenértékű az![]()
![]()
Innen az y(0)=0 feltételt használva c2=-2. Így a kezdetiérték-feladat megoldására rendezés után az
![]()
2-3. kidolgozott feladat.
Oldjuk meg az
differenciálegyenletet!
![]()
(94)
Megoldás: Mivel az egyenlet nem tartalmazza explicit módon az ismeretlen y függvényt, ezért az egyenlet első fokú -re nézve. Az egyszerűbb írásmód kedvéért - mint a 3.2.2 szakaszban - vezessük be az
![]()
![]()
ahol c tetszőleges valós szám.
Ezért az eredeti, (111) differenciálegyenlet y megoldására
![]()
2-4. kidolgozott feladat.
Oldjuk meg az
kezdetiérték-feladatot!
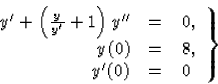
(95)
Megoldás:
Mivel a differenciálegyenlet nem függ explicit módon x-től, ezért úgy
járhatunk el, ahogy a 3.2.4 szakaszban írtuk. Legyen tehát p olyan
függvény, hogy ![]() ; ekkor
; ekkor ![]() .
.
p-t használva differenciálegyenletünk a
![]()
| |
(96) |
(113) valóban egzakt, hiszen
![]()
![]()
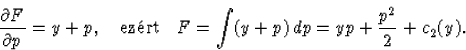
![]()
![]()
| |
(97) |
![]()
| |
(98) |
![]()
y(x)=e-2x+6.
![[*]](nyil_elore.gif)
Készült a SZIF-MML-rendszer felhasználásával